摘要:17.(1)解:由正弦定理得.
网址:http://m.1010jiajiao.com/timu_id_370354[举报]
已知 中,内角
中,内角 的对边的边长分别为
的对边的边长分别为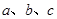 ,且
,且
(I)求角 的大小;
的大小;
(II)若 求
求 的最小值.
的最小值.
【解析】第一问,由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
第二问,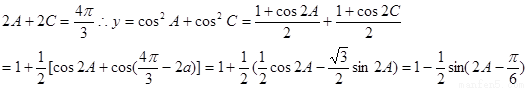
三角函数的性质运用。
解:(Ⅰ)由正弦定理可得:sinBcosC=2sinAcosB-sinCcosB,即sin(B+C)=2sinAcosB,
(Ⅱ)由(Ⅰ)可知
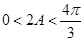 ,
, ,则当
,则当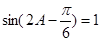 ,即
,即 时,y的最小值为
时,y的最小值为 .
.
查看习题详情和答案>>
给出问题:已知△ABC满足a·cosA=b·cosB,试判断△ABC的形状,某学生的解答如下:
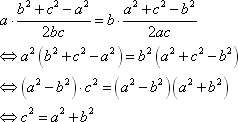
故△ABC事直角三角形.
(ii)设△ABC外接圆半径为R,由正弦定理可得,原式等价于
![]()
故△ABC是等腰三角形.
综上可知,△ABC是等腰直角三角形.
请问:该学生的解答是否正确?若正确,请在下面横线中写出解题过程中主要用到的思想方法;若不正确,请在下面横线中写出你认为本题正确的结果________.
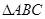 中,
中,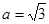 ,
,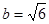 ,
,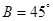 ,解这个三角形;
,解这个三角形;
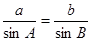
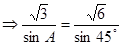 ,然后又
,然后又 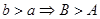
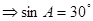
 再又
再又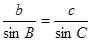 得到c。
得到c。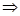
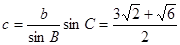


 满足
满足 ,试判定
,试判定 ,
,
 ,
, ,
, 是直角三角形.
是直角三角形.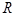 .由正弦定理可得,原式等价于
.由正弦定理可得,原式等价于

 ,
,