摘要：-0+ g(x)0ㄋ
网址：http://m.1010jiajiao.com/timu_id_364750[举报]
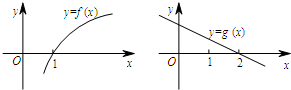函数y=f（x），y=g（x）的图象如下，f（1）=g（2）=0，不等式| f(x) |
| g(x) |
| A、{x|x＜1或x＞2}∪{x|1＜x＜2} |
| B、{x|1≤x＜2} |
| C、{x|x≤1或x＞2}∪{x|1＜x＜2} |
| D、{x|1≤x≤2} |
设函数f（x）=x2+2lnx，用f'（x）表示f（x）的导函数，g(x)=(x2-
)f′(x)，（其中m∈R，且m＞0．）
（1）求函数f（x）的单调区间；
（2）若对任意的x1、x2∈[
，1]都有f'（x1）≤g'（x2）成立，求实数m的取值范围；
（3）试证明：对任意正数a和正整数n，不等式[f'（a）]n-2n-1f'（an）≥2n（2n-2）恒成立．
查看习题详情和答案>>
| m2 |
| 12 |
（1）求函数f（x）的单调区间；
（2）若对任意的x1、x2∈[
| 1 |
| 3 |
（3）试证明：对任意正数a和正整数n，不等式[f'（a）]n-2n-1f'（an）≥2n（2n-2）恒成立．
规定maxf（x），g（x）=
，若定义在R上的奇函数F（x）满足：当x＞0时，F（x）=max1-log2x，1+log2x．
（1）求F（x）的解析式，并写出F（x）的单调区间；
（2）若方程F（x）=m有唯一实数解，求实数m的值；
（3）求t＞0时，函数y=F（x）在x∈[t，2]上的值域． 查看习题详情和答案>>
|
（1）求F（x）的解析式，并写出F（x）的单调区间；
（2）若方程F（x）=m有唯一实数解，求实数m的值；
（3）求t＞0时，函数y=F（x）在x∈[t，2]上的值域． 查看习题详情和答案>>
（2012•开封一模）已知函数f(x)=
，把函数g(x)=f(x)-x的零点按从小到大的顺序排列成一个数列，则该数列的前n项的和为Sn，则S10=（ ）
|
已知函数f(x)=
，函数g(x)=asin(
x)-2a+2（a＞0），若存在x1、x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是（ ）
| 2x2 |
| x+1 |
| π |
| 6 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|