网址:http://m.1010jiajiao.com/timu_id_358888[举报]
一、填空题(本大题满分60分,共12小题,每小题满分5分)
10. 6 11.①⑤ 12. 2
二、选择题(本大题满分16分,共4小题,每小题满分4分)
三、解答题(本大题满分74,共5小题)
17.解:(1)取BC的中点F,连接EF、AF,则EF//PB,
所以∠AEF就是异面直线AE和PB所成角或其补角;
……………3分
∵∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC,
(2)因为E是PC中点,所以E到平面ABC的距离为.files/image114.gif) …………10分
…………10分
18.(本题满分14分)
19.(本题满分14分)
20.(本题满分16分,第1小题满分6分,第2小题满分10分)
雪花曲线的特性是周长无限增大而面积有限的图形。 ………………16分
(第3小题酌情给分)
21.(本题20分,第1小题满分4分,第2小题满分6分,第3小题6分,第4小题4分)
消去
.files/image170.gif) 的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:
的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:.files/image172.gif) ;直线L与椭圆M相切的充要条件为:
;直线L与椭圆M相切的充要条件为:.files/image174.gif) ;直线L与椭圆M相离的充要条件为:
;直线L与椭圆M相离的充要条件为:.files/image176.gif) ……14分
……14分
命题得证。
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
(4)可以类比到双曲线:设F1、F2是双曲线.files/image182.gif) 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线.files/image183.gif) 距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:
距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:.files/image172.gif) ;直线L与双曲线M相切的充要条件为:
;直线L与双曲线M相切的充要条件为:.files/image174.gif) ;直线L与双曲线M相离的充要条件为:
;直线L与双曲线M相离的充要条件为:.files/image176.gif)
………………20分
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
本资料由《七彩教育网》www.7caiedu.cn 提供!
图中的曲线叫雪花曲线(Koch Snowflake),它的生成方法是:
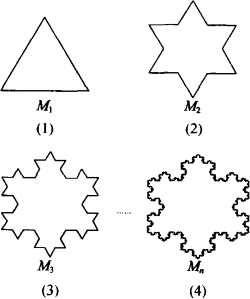
(1)将正三角形图(1)的每边三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边,得到图(2);
(2)将图(2)的每边三等分,重复上述的作图方法,得到图(3);
(3)再按上述方法继续做下去,就可以得到图(4)所示的曲线.
将图(1)、(2)、(3)…中的图形依次记作M1、M2、M3、….
思考1:请分别说出M1、M2、M3的边数,想一想、如何得到M4的边数?
思考2:如果知道了Mn-1的边数,我们能否知道Mn的边数?

(i)将正三角形(图①)的每边三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边,得到图②;
(ii)将图②的每边三等分,重复上述作图方法,得到图③;
(iii)再按上述方法无限多次继续作下去,所得到的曲线就是雪花曲线.
将图①、图②、图③…中的图形依次记作M1、M2、…、Mn…设M1的边长为1.
求:(1)Mn的边数an;
(2)Mn的边长Ln;
(3)Mn的面积Sn的极限.
.files/image100.gif)
.files/image102.gif)
.files/image104.gif)
.files/image106.gif)
.files/image108.gif)
.files/image110.gif)
.files/image112.gif)
.files/image116.gif)
.files/image118.gif)
.files/image120.gif)
.files/image122.gif)
.files/image124.gif)
.files/image126.gif)
.files/image128.gif)
.files/image130.gif)
.files/image132.gif)
.files/image134.gif)
.files/image136.gif)
.files/image138.gif)
.files/image140.gif)
.files/image142.gif)
.files/image144.gif)
.files/image146.gif)
.files/image148.gif)
.files/image150.gif)
.files/image090.gif)
.files/image152.gif)
.files/image154.gif)
.files/image156.gif)
.files/image158.gif)
.files/image160.gif)
.files/image162.gif)
.files/image164.gif)
.files/image166.gif)
.files/image168.gif)
.files/image178.gif)
.files/image180.gif)

