网址:http://m.1010jiajiao.com/timu_id_357929[举报]
2009.5
一、选择题:本大题共10小题,每小题5分,满分50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
D
B
A
C
A
B
C
D
二.填空题:本大题共5小题,考生作答4小题,每小题5分,共20分。第11~13题为必做题,第14~15题,考生只能从中选做两题,若全答只计前一题的得分。
11:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image337.gif) ; 12:甲; 13:
; 12:甲; 13:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image339.gif) ; 14:
; 14:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image082.gif) ; 15:
; 15:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image342.gif) ;
;
解答提示
1.解:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image344.gif) 则
则文科数学Ekaonet20090509asfgeq4gy54yw4.files/image346.gif) ,不符合,
,不符合,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image348.gif) 则
则文科数学Ekaonet20090509asfgeq4gy54yw4.files/image350.gif) ,或
,或文科数学Ekaonet20090509asfgeq4gy54yw4.files/image352.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image354.gif) 则
则文科数学Ekaonet20090509asfgeq4gy54yw4.files/image356.gif) ,成立.
,成立.
2.解:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image358.gif) ,故实部为
,故实部为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image045.gif) .
.
3.解:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image360.gif) ,则
,则文科数学Ekaonet20090509asfgeq4gy54yw4.files/image362.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image364.gif) .
.
4.解:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image366.gif) .
.
5.解:支出在文科数学Ekaonet20090509asfgeq4gy54yw4.files/image086.gif) 元的频率为
元的频率为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image368.gif) .
.文科数学Ekaonet20090509asfgeq4gy54yw4.files/image370.gif) .
.
6.解:由真值表可判断,若文科数学Ekaonet20090509asfgeq4gy54yw4.files/image112.gif) 为假命题,则
为假命题,则 文科数学Ekaonet20090509asfgeq4gy54yw4.files/image372.gif) 至少有一假
至少有一假
7.解:当文科数学Ekaonet20090509asfgeq4gy54yw4.files/image374.gif) ,由
,由文科数学Ekaonet20090509asfgeq4gy54yw4.files/image376.gif) ,当
,当文科数学Ekaonet20090509asfgeq4gy54yw4.files/image378.gif) ,由
,由文科数学Ekaonet20090509asfgeq4gy54yw4.files/image380.gif) ,
, 文科数学Ekaonet20090509asfgeq4gy54yw4.files/image382.gif) .
.
8.解:数形结合,将方程组有实数解,表示为直线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image384.gif) 与圆
与圆文科数学Ekaonet20090509asfgeq4gy54yw4.files/image386.gif) 有公共点,则圆心到
有公共点,则圆心到
直线距离不超过半径:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image388.gif) .
.
9.解:设长方体的同一顶点的三条棱为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image390.gif) ,对角线
,对角线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image156.gif) 在各面上的投影为面对角线长,
在各面上的投影为面对角线长,
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image401.gif) 故
故文科数学Ekaonet20090509asfgeq4gy54yw4.files/image403.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image405.gif) ,故球的表面积:
,故球的表面积:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image407.gif) .
.
10.解:如右图,直线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image409.gif) 和
和文科数学Ekaonet20090509asfgeq4gy54yw4.files/image411.gif) 的交点为
的交点为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image413.gif) ,
,
且文科数学Ekaonet20090509asfgeq4gy54yw4.files/image415.gif) 、
、文科数学Ekaonet20090509asfgeq4gy54yw4.files/image417.gif) ,故所求概率为
,故所求概率为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image419.gif) .
.
11.解:周期文科数学Ekaonet20090509asfgeq4gy54yw4.files/image421.gif) .
.
12. 解:平均数文科数学Ekaonet20090509asfgeq4gy54yw4.files/image423.gif) ,方差
,方差文科数学Ekaonet20090509asfgeq4gy54yw4.files/image425.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image427.gif) ,故甲发挥比乙稳定.
,故甲发挥比乙稳定.
13. 解:已知双曲线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image350.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image430.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image432.gif) ,且不妨设
,且不妨设文科数学Ekaonet20090509asfgeq4gy54yw4.files/image434.gif)
由文科数学Ekaonet20090509asfgeq4gy54yw4.files/image436.gif) 得
得文科数学Ekaonet20090509asfgeq4gy54yw4.files/image438.gif) ,又
,又文科数学Ekaonet20090509asfgeq4gy54yw4.files/image440.gif) ,则
,则文科数学Ekaonet20090509asfgeq4gy54yw4.files/image195.gif) 为直角三角形
为直角三角形
故文科数学Ekaonet20090509asfgeq4gy54yw4.files/image442.gif) .
.
14. 解:曲线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image199.gif) 表示的椭圆标准方程为
表示的椭圆标准方程为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image444.gif) ,可知点
,可知点文科数学Ekaonet20090509asfgeq4gy54yw4.files/image205.gif) 、
、文科数学Ekaonet20090509asfgeq4gy54yw4.files/image207.gif)
椭圆的焦点,故文科数学Ekaonet20090509asfgeq4gy54yw4.files/image446.gif) .
.
15. 解:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image448.gif) 为直径
为直径文科数学Ekaonet20090509asfgeq4gy54yw4.files/image213.gif) 所对的圆周角,则
所对的圆周角,则文科数学Ekaonet20090509asfgeq4gy54yw4.files/image450.gif) ,在
,在文科数学Ekaonet20090509asfgeq4gy54yw4.files/image452.gif) 中,
中,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image454.gif) ,
,
由等面积法有文科数学Ekaonet20090509asfgeq4gy54yw4.files/image456.gif) ,故得
,故得文科数学Ekaonet20090509asfgeq4gy54yw4.files/image458.gif) .
.
三.解答题:本大题共6小题,共80分。解答应写出文字说明、演算步骤或推证过程。
16. (本小题满分12分)
解:(Ⅰ)文科数学Ekaonet20090509asfgeq4gy54yw4.files/image460.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image462.gif) 为锐角,
为锐角,
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image464.gif) ,
,
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image466.gif) ;
…………………4分
;
…………………4分
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image468.gif) ……… 6分
……… 6分
(Ⅱ)由(Ⅰ)可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image470.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image472.gif) ,∴
,∴ 文科数学Ekaonet20090509asfgeq4gy54yw4.files/image474.gif) …………………7分
…………………7分
由正弦定理文科数学Ekaonet20090509asfgeq4gy54yw4.files/image476.gif) ,可得
,可得文科数学Ekaonet20090509asfgeq4gy54yw4.files/image478.gif) …………………9分
…………………9分
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image480.gif) …………………12分
…………………12分
17. (本小题满分12分)
解: (I) 用 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲 表示一种传球方法,(也可用树形图表示,如下图)
甲 表示一种传球方法,(也可用树形图表示,如下图)
所有传球方法共有
甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲
甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙; 甲
乙; 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲
甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙; 甲
丙; 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲; 甲
甲; 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙;
乙;
甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲
甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙; 甲
乙; 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲
甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙; 甲
丙; 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 甲; 甲
甲; 甲文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙
丙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 乙
乙文科数学Ekaonet20090509asfgeq4gy54yw4.files/image482.gif) 丙;
丙;
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image483.gif) 则共有8种传球方法 …………………………………………8分
则共有8种传球方法 …………………………………………8分
(情况列举不足或过剩给4分)
(Ⅱ)记求第3次球恰好传回给甲的事件为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image176.gif) ,
,
由(I)可知共有两种情况,则
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image486.gif) .
…………………………………………12分
.
…………………………………………12分
18.(本小题满分14分)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image488.gif) 证明:(Ⅰ)证法一:取
证明:(Ⅰ)证法一:取文科数学Ekaonet20090509asfgeq4gy54yw4.files/image490.gif) 中点为
中点为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image492.gif) ,连结
,连结文科数学Ekaonet20090509asfgeq4gy54yw4.files/image494.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image496.gif) 中,…………1分
中,…………1分
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image498.gif) ,∴
,∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image500.gif) 且
且文科数学Ekaonet20090509asfgeq4gy54yw4.files/image502.gif) …………2分
…………2分
又∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image504.gif) 且
且文科数学Ekaonet20090509asfgeq4gy54yw4.files/image506.gif) ,
,
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image508.gif) 且
且文科数学Ekaonet20090509asfgeq4gy54yw4.files/image510.gif) …………3分
…………3分
四边形文科数学Ekaonet20090509asfgeq4gy54yw4.files/image512.gif) 为平行四边形,∴
为平行四边形,∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image514.gif) …………4分
…………4分
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image516.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image519.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) ,
,
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image247.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) , ………………7分
, ………………7分
证法二:由图1可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image522.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image524.gif) …………1分
…………1分
折叠之后平行关系不变
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image526.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image528.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) ,
,
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image530.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) ,
,
同理文科数学Ekaonet20090509asfgeq4gy54yw4.files/image532.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) …………4分
…………4分
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image534.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image536.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image538.gif) ,
,
∴平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image540.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) …………6分
…………6分
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image542.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image544.gif) ,∴
,∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image247.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image249.gif) …………7分
…………7分
(Ⅱ)解法1: ∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image546.gif) …………8分
…………8分
由图1可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image548.gif)
∵平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image243.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image245.gif) ,平面
,平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image550.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image552.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image554.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image245.gif) ,
,
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image556.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image239.gif) , …………11分
, …………11分
由图1可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image559.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image561.gif) …………12分
…………12分
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image563.gif)
解法2: 由图1可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image565.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image567.gif)
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image534.gif)
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image570.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image538.gif) ,
…………9分
,
…………9分
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image573.gif)
点文科数学Ekaonet20090509asfgeq4gy54yw4.files/image271.gif) 到平面
到平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image538.gif) 的距离等于点
的距离等于点文科数学Ekaonet20090509asfgeq4gy54yw4.files/image219.gif) 到平面
到平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image538.gif) 的距离为1,…………11分
的距离为1,…………11分
由图1可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image578.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image580.gif) …………12分
…………12分
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image582.gif) ∴
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image584.gif)
解法3: 过文科数学Ekaonet20090509asfgeq4gy54yw4.files/image269.gif) 作
作文科数学Ekaonet20090509asfgeq4gy54yw4.files/image587.gif) ,垂足为
,垂足为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image589.gif) ,…………8分
,…………8分
由图1可知文科数学Ekaonet20090509asfgeq4gy54yw4.files/image548.gif)
∵平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image243.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image245.gif) ,
,
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image550.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image552.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image554.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image245.gif) ,
,
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image556.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image239.gif) ,
,
∵文科数学Ekaonet20090509asfgeq4gy54yw4.files/image591.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image239.gif) ∴
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image594.gif) ,
,
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image596.gif) 平面
平面文科数学Ekaonet20090509asfgeq4gy54yw4.files/image598.gif) …………11分
…………11分
由文科数学Ekaonet20090509asfgeq4gy54yw4.files/image600.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image602.gif) ,
,
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image604.gif) , …………12分
, …………12分
在文科数学Ekaonet20090509asfgeq4gy54yw4.files/image606.gif) 中,由等面积法可得
中,由等面积法可得文科数学Ekaonet20090509asfgeq4gy54yw4.files/image608.gif) …………13分
…………13分
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image610.gif) …………14分
…………14分
19. (本小题满分14分)
解:(Ⅰ) 已知椭圆的短半轴为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image025.gif) ,半焦距为
,半焦距为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image613.gif) ,
,
由离心率等于文科数学Ekaonet20090509asfgeq4gy54yw4.files/image615.gif) …………………………2分
…………………………2分
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image617.gif) ,
…………………………3分
,
…………………………3分
∴椭圆的上顶点文科数学Ekaonet20090509asfgeq4gy54yw4.files/image619.gif) ,∴抛物线的焦点为
,∴抛物线的焦点为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image619.gif) ,
,
∴抛物线的方程为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image621.gif) …………………………6分
…………………………6分
(Ⅱ)设直线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image623.gif) 的方程为
的方程为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image625.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image627.gif) ,
,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image629.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image631.gif) ∴
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image633.gif) ∴切线
∴切线文科数学Ekaonet20090509asfgeq4gy54yw4.files/image273.gif) 、
、文科数学Ekaonet20090509asfgeq4gy54yw4.files/image275.gif) 的斜率分别为
的斜率分别为文科数学Ekaonet20090509asfgeq4gy54yw4.files/image635.gif) 、
、文科数学Ekaonet20090509asfgeq4gy54yw4.files/image637.gif) …………………………8分
…………………………8分
当文科数学Ekaonet20090509asfgeq4gy54yw4.files/image277.gif) 时,
时,文科数学Ekaonet20090509asfgeq4gy54yw4.files/image640.gif) 即:
即:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image642.gif) …………………………9分
…………………………9分
由文科数学Ekaonet20090509asfgeq4gy54yw4.files/image644.gif) 得:
得:文科数学Ekaonet20090509asfgeq4gy54yw4.files/image646.gif)
文科数学Ekaonet20090509asfgeq4gy54yw4.files/image648.gif) 解得
解得文科数学Ekaonet20090509asfgeq4gy54yw4.files/image650.gif) 或
或文科数学Ekaonet20090509asfgeq4gy54yw4.files/image652.gif) ①
①
∴文科数学Ekaonet20090509asfgeq4gy54yw4.files/image654.gif) 即:
即:
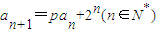
(1)求常数p的值和数列{an}的通项公式;
(2)若抽去数列中的第一项、第四项、第七项、…第3n-2项,…,余下的项按原来的顺序组成一个新的数列{bn},试写出数列
{bn}的通项公式;
(3)在(2)的条件下,设数列{bn}的前n项和为Tn,是否存在正整数n,使得
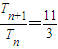 ?若存在,试求所有满足条件的正整数n的值,若不存在,请说明理由.
?若存在,试求所有满足条件的正整数n的值,若不存在,请说明理由.查看习题详情和答案>>
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
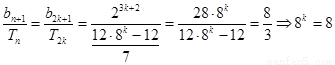
 ,
,
查看习题详情和答案>>
 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.(1) 求常数
 的值和数列
的值和数列 的通项公式;
的通项公式;(2) 若抽去数列
 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;(3) 在(2)的条件下,设数列
 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.文科数学Ekaonet20090509 </div>
<div id=)