摘要:证:直线MN过一定点.
网址:http://m.1010jiajiao.com/timu_id_351827[举报]
已知椭圆C:![]() ,直线
,直线![]() 恒过的定点F为椭圆的一个焦点,且椭圆上的点到焦点F的最大距离为3,
恒过的定点F为椭圆的一个焦点,且椭圆上的点到焦点F的最大距离为3,
(1)求椭圆C的方程;
(2)若直线MN为垂直于x轴的动弦,且M、N均在椭圆C上,定点T(4,0),直线MF与直线NT交于点S
①求证:点S恒在椭圆C上;
②求△MST面积的最大值。
查看习题详情和答案>>给定椭圆C: ,称圆心在原点O、半径为
,称圆心在原点O、半径为 的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为
的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 距离为
距离为 ;
;
(1)、求椭圆C的方程及其“伴椭圆”的方程;
(2)、若倾斜角为 的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
(3)、若点P是椭圆C“伴椭圆”上一动点,过点P作直线 ,使得
,使得 与椭圆C都只有一个公共点,求证:
与椭圆C都只有一个公共点,求证: 。
。
查看习题详情和答案>>
给定椭圆C: ,称圆心在原点O、半径为
,称圆心在原点O、半径为 的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为
的圆是椭圆C的“伴椭圆” ,若椭圆C的一个焦点为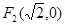 ,其短轴上的一个端点到
,其短轴上的一个端点到 距离为
距离为 ;
;
(1)、求椭圆C的方程及其“伴椭圆”的方程;
(2)、若倾斜角为 的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
的直线与椭圆C只有一个公共点,且与椭圆C的“伴椭圆”相交于M、N两点,求弦MN的长。
(3)、若点P是椭圆C“伴椭圆”上一动点,过点P作直线 ,使得
,使得 与椭圆C都只有一个公共点,求证:
与椭圆C都只有一个公共点,求证: 。
。
查看习题详情和答案>>