摘要:知平面
网址:http://m.1010jiajiao.com/timu_id_350891[举报]
将一块圆心角为
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为
a2,那么请问哪种裁法能得到最大面积的矩形?说明理由.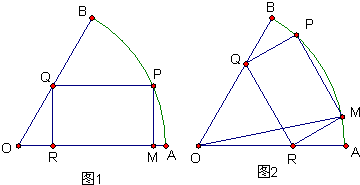
查看习题详情和答案>>
| π |
| 3 |
(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为
| ||
| 6 |

将一块圆心角为 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为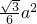 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.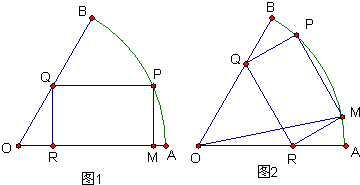
查看习题详情和答案>>
将一块圆心角为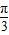 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为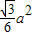 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.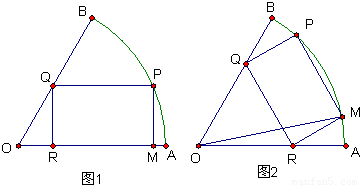
查看习题详情和答案>>
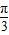 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为
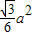 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.
查看习题详情和答案>>
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
查看习题详情和答案>>