题目内容
将一块圆心角为
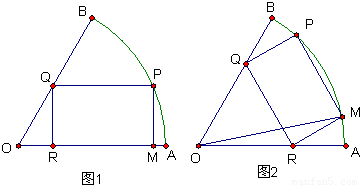
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为
a2,那么请问哪种裁法能得到最大面积的矩形?说明理由.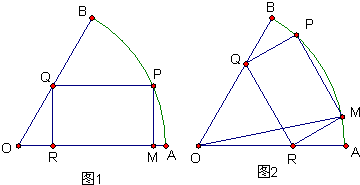
| π |
| 3 |
(1)在图1中,设矩形一边PM的长为x,试把矩形PQRM的面积表示成关于x的函数;
(2)在图2中,设∠AOM=θ,试把矩形PQRM的面积表示成关于θ的函数;
(3)已知按图1的方案截得的矩形面积最大为
| ||
| 6 |

分析:(1)求出PM,RM的值,利用面积公式可得结论;
(2)利用正弦定理求RM,OR,再利用面积公式可得结论;
(3)利用二倍角公式、辅助角公式化简函数求最值,即可得到结论.
(2)利用正弦定理求RM,OR,再利用面积公式可得结论;
(3)利用二倍角公式、辅助角公式化简函数求最值,即可得到结论.
解答:解:(1)PM=QR=x,在Rt△QRO中,OR=
在Rt△PMO中,OM=
,∴RM=OM-OR=
-
…(2分)
∴S=PM•RM=x
-
x2,x∈(0,
a)…(3分)
(2)∠MRA=
×
=
,∠MRO=
,
在△OMR中,由正弦定理,得:
=
,即RM=2a•sinθ,…(6分)
又
=
,∴OR=2a•sin(
-θ),…(8分)
又正△ORQ中,QR=OR=2a•sin(
-θ)
∴矩形的MPQR的面积为S=MR•PQ=4a2•sinθ•sin(
-θ) θ∈(0,
)…(9分)
(3)对于(2)中的函数S=4a2sinθ(
cosθ-
sinθ)=4a2(
sinθcosθ-
sin2θ)=4a2[
sin2θ-
(1-cos2θ)]=2a2[sin(2θ+
)-
]…(11分)
当2θ+
=
,即θ=
时,Smax=(2-
)a2…(13分)
∵(2-
)a2<
a2,故按图1的方案能得到最大面积的矩形.…(14分)
| x | ||
|
在Rt△PMO中,OM=
| a2-x2 |
| a2-x2 |
| ||
| 3 |
∴S=PM•RM=x
| a2-x2 |
| ||
| 3 |
| ||
| 2 |
(2)∠MRA=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
在△OMR中,由正弦定理,得:
| RM |
| sinθ |
| a | ||
sin
|
又
| OR | ||
sin(
|
| a | ||
sin
|
| π |
| 6 |
又正△ORQ中,QR=OR=2a•sin(
| π |
| 6 |
∴矩形的MPQR的面积为S=MR•PQ=4a2•sinθ•sin(
| π |
| 6 |
| π |
| 3 |
(3)对于(2)中的函数S=4a2sinθ(
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 4 |
| π |
| 3 |
| ||
| 2 |
当2θ+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 3 |
∵(2-
| 3 |
| ||
| 6 |
点评:本题考查函数模型的建立,考查正弦定理的运用,考查三角函数的化简,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
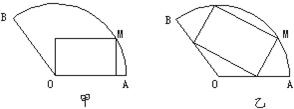 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值. 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)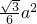 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.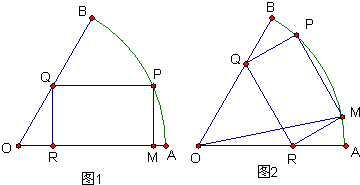
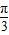 半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)
半径为a的扇形铁片截成一块矩形,如图,有两种裁法:让矩形一边在扇形的一半径OA上(图1)或让矩形一边与弦AB平行(图2)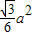 ,那么请问哪种裁法能得到最大面积的矩形?说明理由.
,那么请问哪种裁法能得到最大面积的矩形?说明理由.