摘要:9.. 10.. 11. 52.5%. 12. .
网址:http://m.1010jiajiao.com/timu_id_350838[举报]
把正整数1,2,3,4,5,6,…按某种规律填入下表,
|
查看习题详情和答案>>
(本题9分)给出下面的数表序列:
| 表1 | 表2 | 表3 | … |
| 1 | 1 3 | 1 3 5 | |
| | 4 | 4 8 | |
| | | 12 | |
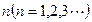 有
有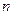 行,第1行的
行,第1行的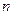 个数
个数 是1,3,5,…,
是1,3,5,…, ,从第2行起,每行中的每个数都等于它肩上的两数之和。
,从第2行起,每行中的每个数都等于它肩上的两数之和。(1)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表
 (不要求证明)
(不要求证明)(2)每个数表中最后一行都只有一个数,它们构成数列1,4,12,…,记此数列为
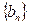 ,求数列
,求数列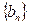 的前
的前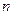 项和
查看习题详情和答案>>
项和
查看习题详情和答案>>
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
(1)利用散点图或相关系数r的大小判断变量y对x是否线性相关?为什么?
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据:
≈25.617,16×11+14×9+12×8+8×5=438,162+142+122+82=660,112+92+82+52=291).
查看习题详情和答案>>
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据:
| 656.25 |
为迎接2010年11至27日在广州举办的第16届亚运会,某高台跳水运动员加强训练,经多次统计与分析,得到t 秒时该运动员相对于水面的高度(单位:m)是h(t)=-4.8t2+8t+10.则该运动员在t=2秒时的瞬时速度为
查看习题详情和答案>>
-11.2
-11.2
m/s,经过2.5
2.5
秒后该运动员落入水中.一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
(1)利用散点图或相关系数r的大小判断变量y对x是否线性相关?为什么?
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据:
≈25.617,16×11+14×9+12×8+8×5=438,162+142+122+82=660,112+92+82+52=291).
查看习题详情和答案>>
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(最后结果精确到0.001.参考数据:
| 656.25 |