题目内容
(理科)如图的多面体是底面为平行四边形的直四棱柱ABCD-A1B1C1D1,经平面AEFG所截后得到的图形.其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
(Ⅰ)求证:BD⊥平面ADG;
(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值.
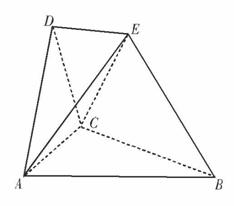
(文科)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(Ⅰ)求证:AF⊥平面CBF;
(Ⅱ)设FC的中点为M,求证:OM∥平面DAF.

【答案】分析:(理科)(I)由题在△BAD中,通过计算得到AD⊥BD,再利用条件线面垂直得到线线垂直,进而得到要证的线面垂直;
(II) 由题意及图形特点建立如图的空间直角坐标系,利用平面的法向量的夹角与二面角的大小之间的关系求出二面角的大小.
(文科)(I)由题意及平面ABCD⊥平面ABEF且CB⊥AB,利用面面垂直的性质定理得到线面垂直,在利用圆的直径所对的圆周角为直角的性质得到线线垂直,进而利用线面垂直的判定定理得出要证明的结论;
(II)由题意及条件借助线线平行得到线面平行,再利用线面平行的性质定理的得到所证.
解答:(理科)解:(Ⅰ)证明:在△BAD中,AB=2AD=2,∠BAD=60°,
由余弦定理得,BD=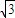 ∴AB2=AD2+BD2.
∴AB2=AD2+BD2.
∴AD⊥BD
又GD⊥平面ABCD
∴GD⊥BD,
GD∩AD=D,
∴BD⊥平面ADG,
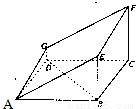 (Ⅱ)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz
(Ⅱ)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz
则有A(1,0,0),B(0,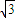 ,0),G(0,0,1),E(0,
,0),G(0,0,1),E(0,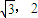 )
)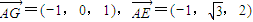
设平面AEFG法向量为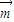 =(x,y,z)
=(x,y,z)
则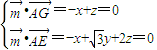 ,
,
取 ,
,
平面ABCD的一个法向量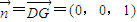 ,
,
设面ABFG与面ABCD所成锐二面角为θ,
则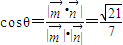 .
.
 (文科)解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,
(文科)解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF,
∵AF?平面ABEF,∴AF⊥CB,
又∵AB为圆O的直径,∴AF⊥BF,∴AF⊥平面CBF.
(Ⅱ)设DF的中点为N,则MN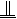
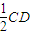 ,又AO
,又AO
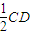 ,则MN
,则MN AO,MNAO为平行四边形,
AO,MNAO为平行四边形,
∴OM∥AN,又AN?平面DAF,OM?平面DAF,∴OM∥平面DAF.
点评:(理科)此题重点考查了线面垂直的判定定理及性质定理等知识,还考查了利用空间向量的知识求解二面角的大小的知识.
(文科)此题重点考查了面卖弄垂直的判定定理及线面垂直的判定定理,还考查了线面平行的判定定理及平行直线间的平行具有传递性.
(II) 由题意及图形特点建立如图的空间直角坐标系,利用平面的法向量的夹角与二面角的大小之间的关系求出二面角的大小.
(文科)(I)由题意及平面ABCD⊥平面ABEF且CB⊥AB,利用面面垂直的性质定理得到线面垂直,在利用圆的直径所对的圆周角为直角的性质得到线线垂直,进而利用线面垂直的判定定理得出要证明的结论;
(II)由题意及条件借助线线平行得到线面平行,再利用线面平行的性质定理的得到所证.
解答:(理科)解:(Ⅰ)证明:在△BAD中,AB=2AD=2,∠BAD=60°,
由余弦定理得,BD=
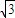 ∴AB2=AD2+BD2.
∴AB2=AD2+BD2.∴AD⊥BD
又GD⊥平面ABCD
∴GD⊥BD,
GD∩AD=D,
∴BD⊥平面ADG,
 (Ⅱ)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz
(Ⅱ)以D为坐标原点,OA为x轴,OB为y轴,OG为z轴建立空间直角坐标系D-xyz则有A(1,0,0),B(0,
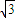 ,0),G(0,0,1),E(0,
,0),G(0,0,1),E(0,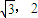 )
)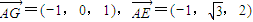
设平面AEFG法向量为
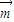 =(x,y,z)
=(x,y,z)则
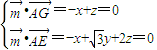 ,
,取
 ,
,平面ABCD的一个法向量
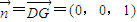 ,
,设面ABFG与面ABCD所成锐二面角为θ,
则
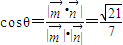 .
. (文科)解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,
(文科)解:(Ⅰ)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF,
∵AF?平面ABEF,∴AF⊥CB,
又∵AB为圆O的直径,∴AF⊥BF,∴AF⊥平面CBF.
(Ⅱ)设DF的中点为N,则MN
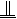
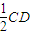 ,又AO
,又AO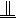
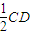 ,则MN
,则MN AO,MNAO为平行四边形,
AO,MNAO为平行四边形,∴OM∥AN,又AN?平面DAF,OM?平面DAF,∴OM∥平面DAF.
点评:(理科)此题重点考查了线面垂直的判定定理及性质定理等知识,还考查了利用空间向量的知识求解二面角的大小的知识.
(文科)此题重点考查了面卖弄垂直的判定定理及线面垂直的判定定理,还考查了线面平行的判定定理及平行直线间的平行具有传递性.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目


 (理科做)如右图,多面体是过正四棱柱的底面正方形ABCD的顶点A作截面AB1C1D1而截得的,且BB1=DD1,已知截面AB1C1D1与底面成30°的二面角,AB=1,则这个多面体的体积为( )
(理科做)如右图,多面体是过正四棱柱的底面正方形ABCD的顶点A作截面AB1C1D1而截得的,且BB1=DD1,已知截面AB1C1D1与底面成30°的二面角,AB=1,则这个多面体的体积为( )