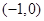摘要:19.(1)方法一:分离参数..变成求函数的最小值. 方法二:利用二次函数的知识解不等式. (2)的根不在之间即可.当.的零点不在之间.
网址:http://m.1010jiajiao.com/timu_id_345558[举报]
(选做题)请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.
A.选修4-1(几何证明选讲)已知AD为圆O的直径,直线BA与圆O相切与点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
(Ⅰ)求证:BA•DC=GC•AD;(Ⅱ)求BM.
B.选修4-4(坐标系与参数方程)求直线 (t为参数)被曲线
(t为参数)被曲线 所截的弦长.
所截的弦长.
C.选修4-5(不等式选讲)(Ⅰ)求函数 的最大值;
的最大值;
(Ⅱ)已知a≠b,求证:a4+6a2b2+b4>4ab(a2+b2).
 查看习题详情和答案>>
查看习题详情和答案>>
A.选修4-1(几何证明选讲)已知AD为圆O的直径,直线BA与圆O相切与点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
(Ⅰ)求证:BA•DC=GC•AD;(Ⅱ)求BM.
B.选修4-4(坐标系与参数方程)求直线
 (t为参数)被曲线
(t为参数)被曲线 所截的弦长.
所截的弦长.C.选修4-5(不等式选讲)(Ⅰ)求函数
 的最大值;
的最大值;(Ⅱ)已知a≠b,求证:a4+6a2b2+b4>4ab(a2+b2).
 查看习题详情和答案>>
查看习题详情和答案>>
(理科做)
阅读下面题目的解法,再根据要求解决后面的问题.
阅读题目:对于任意实数a1,a2,b1,b2,证明不等式(a1b1+a2b2)2≤(a12+a22)(b12+b22).
证明:构造函数f(x)=(a1x+b1)2+(a2x+b2)2=(a12+a22)x2+2(a1b1+a2b2)x+(b12+b22).
注意到f(x)≥0,所以△=[2(a1b1+a2b2)]2-4(a12+a22)(b12+b22)≤0,
即(a1b1+a2b2)2≤(a12+a22)(b12+b22).
(其中等号成立当且仅当a1x+b1=a2x+b2=0,即a1b2=a2b1.)
问题:(1)请用这个不等式证明:对任意正实数a,b,x,y,不等式 成立.
成立.
(2)用(1)中的不等式求函数 的最小值,并指出此时x的值.
的最小值,并指出此时x的值.
(3)根据阅读题目的证明,将不等式(a1b1+a2b2)2≤(a12+a22)(b12+b22)进行推广,得到一个更一般的不等式,并用构造函数的方法对你的推广进行证明.
查看习题详情和答案>>
已知函数 其中
其中 为自然对数的底数,
为自然对数的底数,
 .(Ⅰ)设
.(Ⅰ)设 ,求函数
,求函数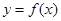 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问中,当 时,
时, ,
, .结合表格和导数的知识判定单调性和极值,进而得到最值。
.结合表格和导数的知识判定单调性和极值,进而得到最值。
第二问中,∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即
分离参数的思想求解参数的范围
解:(Ⅰ)当 时,
时, ,
, .
.
当 在
在 上变化时,
上变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
1/e |
∴ 时,
时, ,
, .
.
(Ⅱ)∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即 .
.
∴对于任意的 ,原不等式恒成立,等价于
,原不等式恒成立,等价于 对
对 恒成立,
恒成立,
∵对于任意的 时,
时, 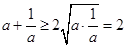 (当且仅当
(当且仅当 时取等号).
时取等号).
∴只需 ,即
,即 ,解之得
,解之得 或
或 .
.
因此, 的取值范围是
的取值范围是
查看习题详情和答案>>