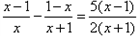摘要：17．B(提示:先将各方程整理为一般式.再利用根的判别式进行判断.B项中＜0.所以B项方程无实数根)

网址：http://m.1010jiajiao.com/timu_id_342521[举报]

先阅读下面解方程
x-1
x
-
1-x
x+1
=
5x-5
2x+2
的过程，然后回答后面的问题．
解：将原方程整理为：
x-1
x
+
x-1
x+1
=
5(x-1)
2(x+1)
（第一步）
方程两边同除以（x-1）得：
1
x
+
1
x+1
=
5
2(x+1)
（第二步）
去分母，得：2（x+1）+2x=5x（第三步）
解这个方程，得：x=2（第四步）
在上面的解题过程中：
（1）第三步变形的依据是
等式的性质
等式的性质
；
（2）出现错误的一步是
第二步
第二步
；
（3）上述解题过程缺少的一步是
检验
检验
；写出这个方程的完整的解题过程．
 查看习题详情和答案>>
先阅读下面解方程
x-1
x
-
1-x
x+1
=
5x-5
2x+2
的过程，然后回答后面的问题：
解：第一步：将原方程整理为
x-1
x
-
1-x
x+1
=
5(x-1)
2(x+1)

第二步：方程两边同除以（x-1），得
1
x
-
1
x+1
=
5
2(x+1)

第三步：去分母，得2（x+1）+2x=5x．
第四步：解这个整式方程得x=2．
上面解题过程中：
（1）第三步变形的依据是
分式的基本性质
分式的基本性质
；
（2）出现错误的一步是
第二步
第二步
；
（3）上述解题过程中还缺少的一步是
检验
检验
；
（4）方程除了有解x=2还有其他的解吗？如有，请直接写出另外的解
x=1
x=1
．
 查看习题详情和答案>>

先阅读下面解方程的过程，然后回答后面的问题。
解：将原方程整理为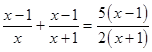：（第一步）
方程两边同除以（x－1）得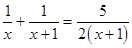： （第二步）
去分母，得：2（x＋1）＋2x=5x（第三步）
解这个方程，得：x=2（第四步）
在上面的解题过程中：
【小题1】第三步变形的依据是               
【小题2】出现错误的一步是                
【小题3】上述解题过程缺少的一步是                      （2分）
写出这个方程的完整的解题过程

 查看习题详情和答案>>

先阅读下面解方程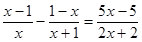的过程，然后回答后面的问题。

解：将原方程整理为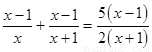：（第一步）

方程两边同除以（x－1）得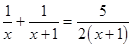： （第二步）

去分母，得：2（x＋1）＋2x=5x（第三步）

解这个方程，得：x=2（第四步）

在上面的解题过程中：

1.第三步变形的依据是               

2.出现错误的一步是                

3.上述解题过程缺少的一步是                       （2分）

写出这个方程的完整的解题过程

 

 查看习题详情和答案>>

先阅读下面解方程的过程，然后回答后面的问题。
解：第一步：将原方程整理为    
第二步：方程两边同除以（x-1），得
第三步：去分母，得2（x+1）+2x=5x
第四步：解这个整式方程得x=2。
上面解题过程中：    
（1）第三步变形的依据是                       。    
（2）出现错误的一步是                        。    
（3）上述解题过程中还缺少的一步是                   。    
（4）方程的正确解为          。

查看习题详情和答案>>