摘要:即当时,等式也成立 ----------------13分
网址:http://m.1010jiajiao.com/timu_id_340212[举报]
在数列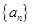 中,
中,
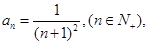 记
记
(Ⅰ)求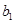 、
、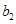 、
、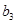 、
、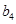 并推测
并推测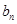 ;
;
(Ⅱ)用数学归纳法证明你的结论.
【解析】第一问利用递推关系可知,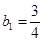 、
、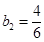 、
、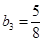 、
、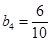 ,猜想可得
,猜想可得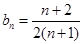
第二问中,①当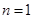 时,
时,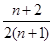 =
=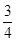 ,又
,又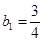 ,猜想正确
,猜想正确
②假设当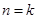 时猜想成立,即
时猜想成立,即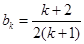 ,
,
当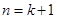 时,
时,
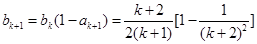 =
=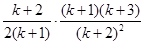
=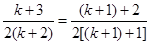 ,即当
,即当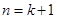 时猜想也成立
时猜想也成立
两步骤得到。
(2)①当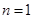 时,
时,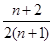 =
=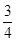 ,又
,又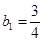 ,猜想正确
,猜想正确
②假设当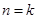 时猜想成立,即
时猜想成立,即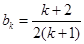 ,
,
当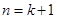 时,
时,
 =
=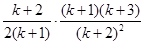
=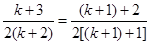 ,即当
,即当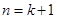 时猜想也成立
时猜想也成立
由①②可知,对于任何正整数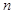 都有
都有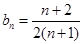 成立
成立
查看习题详情和答案>>
已知命题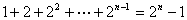 及其证明:
及其证明:
(1)当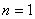 时,左边=1,右边=
时,左边=1,右边=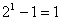 所以等式成立;
所以等式成立;
(2)假设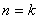 时等式成立,即
时等式成立,即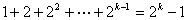 成立,
成立,
则当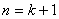 时,
时,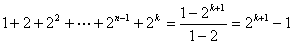 ,所以
,所以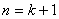 时等式也成立。
时等式也成立。
由(1)(2)知,对任意的正整数n等式都成立。
经判断以上评述
A.命题、推理都正确 B命题不正确、推理正确
C.命题正确、推理不正确 D命题、推理都不正确
查看习题详情和答案>>
 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
. ,
, ,证明
,证明 (
( 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q. ,得
,得 ,
, ,
, .
. ,解得
,解得
 ,
, ,
, .
. ①
① ②
②



 ,
,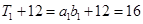 ,
, ,故等式成立.
,故等式成立. ,则当n=k+1时,有:
,则当n=k+1时,有:





 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立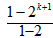 =2k+1-1,所以n=k+1时等式也成立,
=2k+1-1,所以n=k+1时等式也成立,