网址:http://m.1010jiajiao.com/timu_id_340211[举报]
(12分)设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,![]() )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线![]() 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
围.
查看习题详情和答案>>(本题12分)已知函数 有如下性质:如果常数
有如下性质:如果常数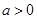 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
(1)如果函数 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;
(2)当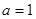 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。
(3)设常数 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值;
查看习题详情和答案>>
(本题12分)已知函数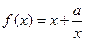 有如下性质:如果常数
有如下性质:如果常数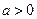 ,那么该函数在
,那么该函数在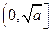 上是减函数,在
上是减函数,在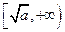 上是增函数;
上是增函数;
(1)如果函数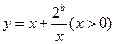 在
在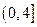 上是减函数,在
上是减函数,在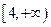 上是增函数,求
上是增函数,求 的值;
的值;
(2)当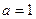 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。
(3)设常数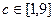 ,求函数
,求函数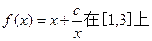 的最大值和最小值;
的最大值和最小值;
(本题12分)已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数;
上是增函数;
(1)如果函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,求
上是增函数,求![]() 的值;
的值;
(2)当![]() 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在![]() 上是减函数。
上是减函数。
(3)设常数![]() ,求函数
,求函数![]() 的最大值和最小值;
的最大值和最小值;
(本小题12分)
在某个以旅游业为主的地区,每年各个月份从事旅游服务工作的人数会发生周期性变化.现假设该地区每年各个月份从事旅游服务工作的人数![]() 可近似地用函数
可近似地用函数![]() 来刻画.其中:正整数
来刻画.其中:正整数![]() 表示月份且
表示月份且![]() ,例如
,例如![]() 时表示1月份;
时表示1月份;![]() 和
和![]() 是正整数;
是正整数;![]() .
.
统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
①各年相同的月份,该地区从事旅游服务工作的人数基本相同;
②该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;
③2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.
(I)试根据已知信息,确定一个符合条件的![]() 的表达式;
的表达式;
(II)一般地,当该地区从事旅游服务工作的人数超过400人时,该地区进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.
查看习题详情和答案>>