网址:http://m.1010jiajiao.com/timu_id_33791[举报]
一、选择题:本大题共10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
D
A
B
B
C
D
二、填空题:本大题7小题,每小题4分,共28分.
11、 ; 12、
; 12、  ; 13、
; 13、 ; 14、
; 14、 ; 15、
; 15、 ; 16、
; 16、 ;17、
;17、 。
。
三、解答题
18、(1)略 ……………………………………………………………………(7分)
(2) 就是二面角
就是二面角 的平面角,即
的平面角,即 ,
,
 …………………………………………………………………(9分)
…………………………………………………………………(9分)
取 中点
中点 ,则
,则 平面
平面 ,
,
 就是
就是 与平面
与平面 所成的角。 …………………………(11分)
所成的角。 …………………………(11分)
 ,
, ,
,
所以 与平面
与平面 所成的角的大小为
所成的角的大小为 。 …………………………(14分)
。 …………………………(14分)
(用向量方法,相应给分)
19、(1) ,
, ,
, …………(7分)
…………(7分)
(2) ,当
,当 时,
时, ;当
;当 时,
时,
 ,而
,而 ,
,
 ……………………………………………(14分)
……………………………………………(14分)
20、(1)当 ,当k=1时,
,当k=1时,
 ……………………………………… (7分)
……………………………………… (7分)
(2)由已知 ,又设
,又设 ,则
,则
 ,
,
知当 时,
时, 为增函数,则知
为增函数,则知 为增函数。…………………(14分)
为增函数。…………………(14分)
(用导数法相应给分)
21、.解:(1)、设 ,则
,则 ,
,
∵点P分 所成的比为
所成的比为 ∴
∴  ∴
∴ 
∴ 代入
代入 中,得
中,得 为P点的轨迹方程.
为P点的轨迹方程.
当 时,轨迹是圆. …………………………………………………(7分)
时,轨迹是圆. …………………………………………………(7分)
(2)、由题设知直线l的方程为 , 设
, 设
联立方程组 ,消去
,消去 得:
得:
∵ 方程组有两解 ∴  且
且 ∴
∴ 或
或 且
且
∵
 ∴
∴
又 ∵  ∴
∴  解得
解得 (舍去)或
(舍去)或
∴ 曲线C的方程是 ……………………………………………(14分)
……………………………………………(14分)
22、解(1) ………………………………………………(5分)
………………………………………………(5分)
猜想  , …………………………………………………………(7分)
, …………………………………………………………(7分)
证明(略) ……………………………………………………………………(10分)
(2) ,要使
,要使 恒成立,
恒成立,
 恒成立
恒成立
即 恒成立.
恒成立.
(i)当 为奇数时,即
为奇数时,即 恒成立, 又
恒成立, 又 的最小值为1,
的最小值为1,
(ii)当 为偶数时,即
为偶数时,即 恒成立, 又
恒成立, 又 的最大值为
的最大值为 ,
,
 即
即 ,又
,又 ,
, 为整数,
为整数,
∴ ,使得对任意
,使得对任意 ,都有
,都有 …………………………………( 16分)
…………………………………( 16分)
平面直角坐标系内的向量都可以用一有序实数对唯一表示,这使我们想到可以用向量作为解析几何的研究工具.如图,设直线
l的倾斜角为α(α≠90°).在l上任取两个不同的点 ,
, ,不妨设向量
,不妨设向量 的方向是向上的,那么向量
的方向是向上的,那么向量 的坐标是(
的坐标是( ).过原点作向量
).过原点作向量 ,则点P的坐标是(
,则点P的坐标是( ),而且直线OP的倾斜角也是α.根据正切函数的定义得
),而且直线OP的倾斜角也是α.根据正切函数的定义得
 ,
,
这就是《数学
2》中已经得到的斜率公式.上述推导过程比《数学2》中的推导简捷.你能用向量作为工具讨论一下直线的有关问题吗?例如:(1)
过点 ,平行于向量
,平行于向量 的直线方程;
的直线方程;
(2)
向量(A,B)与直线 的关系;
的关系;
(3)
设直线 和
和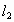 的方程分别是
的方程分别是
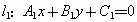

那么,
 ∥
∥ ,
, 的条件各是什么?如果它们相交,如何得到它们的夹角公式?
的条件各是什么?如果它们相交,如何得到它们的夹角公式?
(4)
点 到直线
到直线 的距离公式如何推导?
的距离公式如何推导?

已知曲线C:![]()
(1)由曲线C上任一点E向x轴作垂线,垂足为F,点P分![]() 所成的比为
所成的比为![]() ,问:点P的轨迹可能是圆吗?请说明理由;
,问:点P的轨迹可能是圆吗?请说明理由;
(2)如果直线l的一个方向向量为![]() ,且过点M(0,-2),直线l交曲线C于A、B两点,又
,且过点M(0,-2),直线l交曲线C于A、B两点,又![]() ,求曲线C的方程.
,求曲线C的方程.
(本小题满分12分)已知曲线C:![]()
(1)由曲线C上任一点E向x轴作垂线,垂足为F,点P分![]() 所成的比为
所成的比为![]() ,问:点P的轨迹可能是圆吗?请说明理由;
,问:点P的轨迹可能是圆吗?请说明理由;
如果直线l的一个方向向量为![]() ,且过点M(0,-2),直线l交曲线C于A、B两点,又
,且过点M(0,-2),直线l交曲线C于A、B两点,又![]() ,求曲线C的方程.
,求曲线C的方程.
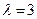 及对应的一个特征向量
及对应的一个特征向量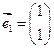 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点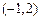 变换成
变换成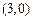 ,求矩阵M。
,求矩阵M。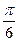 的直线
的直线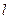 与圆C:
与圆C: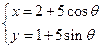 (
(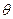 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定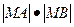 的值。
的值。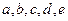 满足
满足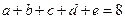 ,
,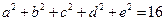 ,试确定
,试确定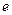 的最大值。
的最大值。 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 ,求矩阵M。
,求矩阵M。 的直线
的直线 与圆C:
与圆C: (
( 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定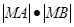 的值。
的值。 满足
满足 ,
, ,试确定
,试确定 的最大值。
的最大值。