摘要：∵l1⊥l2.∴l2的方程为由得

网址：http://m.1010jiajiao.com/timu_id_336548[举报]

已知直线l₁：x-y=0，l₂：x+y=0，点P是线性约束条件

所表示区域内一动点，PM⊥l₁，PN⊥l₂，垂足分别为M、N，且S△OMN=

（O为坐标原点）．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）是否存在过点（2，0）的直线l与（Ⅰ）中轨迹交于点A、B，线段AB的垂直平分线交y轴于Q点，且使得△ABQ是等边三角形．若存在，求出直线l的方程，若不存在，说明理由．

查看习题详情和答案>>

已知直线l₁：x-y=0，l₂：x+y=0，点P是线性约束条件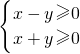 $数学公式$ 所表示区域内一动点，PM⊥l₁，PN⊥l₂，垂足分别为M、N，且 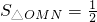$数学公式$ （O为坐标原点）．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）是否存在过点（2，0）的直线l与（Ⅰ）中轨迹交于点A、B，线段AB的垂直平分线交y轴于Q点，且使得△ABQ是等边三角形．若存在，求出直线l的方程，若不存在，说明理由．

查看习题详情和答案>>

已知直线l₁：x-y=0，l₂：x+y=0，点P是线性约束条件

所表示区域内一动点，PM⊥l₁，PN⊥l₂，垂足分别为M、N，且S△OMN=

（O为坐标原点）．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）是否存在过点（2，0）的直线l与（Ⅰ）中轨迹交于点A、B，线段AB的垂直平分线交y轴于Q点，且使得△ABQ是等边三角形．若存在，求出直线l的方程，若不存在，说明理由．

查看习题详情和答案>>

已知直线l₁：x-y=0，l₂：x+y=0，点P是线性约束条件

所表示区域内一动点，PM⊥l₁，PN⊥l₂，垂足分别为M、N，且

（O为坐标原点）．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）是否存在过点（2，0）的直线l与（Ⅰ）中轨迹交于点A、B，线段AB的垂直平分线交y轴于Q点，且使得△ABQ是等边三角形．若存在，求出直线l的方程，若不存在，说明理由．
查看习题详情和答案>>

已知抛物线C：x²=4y的焦点为F，过点F作直线l交抛物线C于A、B两点；椭圆E的中心在原点，焦点在x轴上，点F是它的一个顶点，且其离心率e=

．
（1）求椭圆E的方程；
（2）经过A、B两点分别作抛物线C的切线l₁、l₂，切线l₁与l₂相交于点M．证明：AB⊥MF；
（3）椭圆E上是否存在一点M′，经过点M′作抛物线C的两条切线M′A′、M′B（A′、B′为切点），使得直线A′B′过点F？若存在，求出抛物线C与切线M′A′、M′B所围成图形的面积；若不存在，试说明理由．查看习题详情和答案>>