摘要:所以当时.f(x)在区间[0.1]上单调递减.
网址:http://m.1010jiajiao.com/timu_id_33486[举报]
已知 .
.
(1)求 的单调区间;
的单调区间;
(2)证明:当 时,
时, 恒成立;
恒成立;
(3)任取两个不相等的正数 ,且
,且 ,若存在
,若存在 使
使 成立,证明:
成立,证明: .
.
【解析】(1)g(x)=lnx+ ,
, =
=
 (1’)
(1’)
当k 0时,
0时, >0,所以函数g(x)的增区间为(0,+
>0,所以函数g(x)的增区间为(0,+ ),无减区间;
),无减区间;
当k>0时, >0,得x>k;
>0,得x>k; <0,得0<x<k∴增区间(k,+
<0,得0<x<k∴增区间(k,+ )减区间为(0,k)(3’)
)减区间为(0,k)(3’)
(2)设h(x)=xlnx-2x+e(x 1)令
1)令 = lnx-1=0得x=e, 当x变化时,h(x),
= lnx-1=0得x=e, 当x变化时,h(x), 的变化情况如表
的变化情况如表
|
x |
1 |
(1,e) |
e |
(e,+ |
|
|
|
- |
0 |
+ |
|
h(x) |
e-2 |
|
0 |
↗ |
所以h(x) 0, ∴f(x)
0, ∴f(x) 2x-e
(5’)
2x-e
(5’)
设G(x)=lnx- (x
(x 1)
1)  =
= =
=
 0,当且仅当x=1时,
0,当且仅当x=1时, =0所以G(x) 为减函数, 所以G(x)
=0所以G(x) 为减函数, 所以G(x)  G(1)=0, 所以lnx-
G(1)=0, 所以lnx-
 0所以xlnx
0所以xlnx
 (x
(x 1)成立,所以f(x)
1)成立,所以f(x) 
 ,综上,当x
,综上,当x 1时, 2x-e
1时, 2x-e f(x)
f(x)
 恒成立.
恒成立.
(3) ∵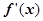 =lnx+1∴lnx0+1=
=lnx+1∴lnx0+1= =
= ∴lnx0=
∴lnx0=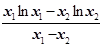 -1
∴lnx0 –lnx
-1
∴lnx0 –lnx =
= -1–lnx
-1–lnx =
= =
= =
= (10’) 设H(t)=lnt+1-t(0<t<1),
(10’) 设H(t)=lnt+1-t(0<t<1),
 =
= =
=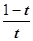 >0(0<t<1), 所以H(t) 在(0,1)上是增函数,并且H(t)在t=1处有意义, 所以H(t)
<H(1)=0∵
>0(0<t<1), 所以H(t) 在(0,1)上是增函数,并且H(t)在t=1处有意义, 所以H(t)
<H(1)=0∵ ∴
∴ =
=
∴lnx0 –lnx >0, ∴x0 >x
>0, ∴x0 >x
查看习题详情和答案>>
下列四个命题:
①函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
②已知函数f(x)=log3x+2,(x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值是13;
③y=x2-2|x|-3的递增区间为[1,+∞);
④已知函数f(x)满足:当x≥3时,f(x)=(
)x;当x<3时,f(x)=f(x+1),则f(1+log34)的值是
.
其中正确命题是 .
查看习题详情和答案>>
①函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
②已知函数f(x)=log3x+2,(x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值是13;
③y=x2-2|x|-3的递增区间为[1,+∞);
④已知函数f(x)满足:当x≥3时,f(x)=(
| 1 |
| 3 |
| 1 |
| 36 |
其中正确命题是
下列四个命题:
①函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
②已知函数f(x)=log3x+2,(x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值是13;
③y=x2-2|x|-3的递增区间为[1,+∞);
④已知函数f(x)满足:当x≥3时,f(x)=(
)x;当x<3时,f(x)=f(x+1),则f(1+log34)的值是
.
其中正确命题是 ______.
查看习题详情和答案>>
①函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
②已知函数f(x)=log3x+2,(x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值是13;
③y=x2-2|x|-3的递增区间为[1,+∞);
④已知函数f(x)满足:当x≥3时,f(x)=(
| 1 |
| 3 |
| 1 |
| 36 |
其中正确命题是 ______.

 ↘
↘ ;当x<3时,f(x)=f(x+1),则f(1+log34)的值是
;当x<3时,f(x)=f(x+1),则f(1+log34)的值是 .
.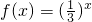 ;当x<3时,f(x)=f(x+1),则f(1+log34)的值是
;当x<3时,f(x)=f(x+1),则f(1+log34)的值是 .
.