题目内容
下列四个命题:
①函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
②已知函数f(x)=log3x+2,(x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值是13;
③y=x2-2|x|-3的递增区间为[1,+∞);
④已知函数f(x)满足:当x≥3时,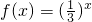 ;当x<3时,f(x)=f(x+1),则f(1+log34)的值是
;当x<3时,f(x)=f(x+1),则f(1+log34)的值是 .
.
其中正确命题是 ________.
③④
分析:①此命题是假命题,举反例说明命题错误;
②由3大于1得到对数函数为增函数,求出y的最大值即可判断真假;
③讨论x的正负化简绝对值,然后利用二次函数的图象找出函数的增区间即可判断此命题的真假;
④根据函数的递推式得到x=1+log34小于3时代入f(x)=f(x+1),得到2+log34大于3即可代入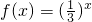 ,求出值即可判断.
,求出值即可判断.
解答:①举一个例子y=- ,当x<0时,函数为增函数,当x>0时,函数为增函数,但是在x≠0时,函数不单调,所以错误;
,当x<0时,函数为增函数,当x>0时,函数为增函数,但是在x≠0时,函数不单调,所以错误;
②由x∈[1,9],又f(x)=log3x+2,所以y=[f(x)]2+f(x2)=[log3x+2]2+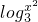 +2,根据3>1得到对数函数log3x为增函数,所以分别当x=9时log3x和
+2,根据3>1得到对数函数log3x为增函数,所以分别当x=9时log3x和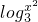 达到最大即y取最大.则y最大=(log39+2)2+log381+2=22,所以此命题错;
达到最大即y取最大.则y最大=(log39+2)2+log381+2=22,所以此命题错;
③当x>0时,y=x2-2x-3,为对称轴为直线x=1的开口向上的抛物线,所以[1,+∞)为函数的增区间;当x<0时,y=x2+2x-3,为对称轴为直线x=-1的开口向上的抛物线,所以(-1,+∞)为增区间,综上,函数y的增区间为[1,+∞),正确;
④因为1+log34<3,所以f(1+log34)=f(1+1+log34),而2+log34>3,所以f(2+log34)=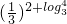 =
= ×
× =
= ,命题正确.
,命题正确.
所以正确命题的序号是③④
故答案为:③④
点评:此题是一道综合题,要求学生掌握二次函数和对数函数的增减性,灵活运用对数函数的运算性质,会利用举反例的方法说明一个命题是假命题.
分析:①此命题是假命题,举反例说明命题错误;
②由3大于1得到对数函数为增函数,求出y的最大值即可判断真假;
③讨论x的正负化简绝对值,然后利用二次函数的图象找出函数的增区间即可判断此命题的真假;
④根据函数的递推式得到x=1+log34小于3时代入f(x)=f(x+1),得到2+log34大于3即可代入
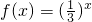 ,求出值即可判断.
,求出值即可判断.解答:①举一个例子y=-
 ,当x<0时,函数为增函数,当x>0时,函数为增函数,但是在x≠0时,函数不单调,所以错误;
,当x<0时,函数为增函数,当x>0时,函数为增函数,但是在x≠0时,函数不单调,所以错误;②由x∈[1,9],又f(x)=log3x+2,所以y=[f(x)]2+f(x2)=[log3x+2]2+
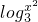 +2,根据3>1得到对数函数log3x为增函数,所以分别当x=9时log3x和
+2,根据3>1得到对数函数log3x为增函数,所以分别当x=9时log3x和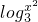 达到最大即y取最大.则y最大=(log39+2)2+log381+2=22,所以此命题错;
达到最大即y取最大.则y最大=(log39+2)2+log381+2=22,所以此命题错;③当x>0时,y=x2-2x-3,为对称轴为直线x=1的开口向上的抛物线,所以[1,+∞)为函数的增区间;当x<0时,y=x2+2x-3,为对称轴为直线x=-1的开口向上的抛物线,所以(-1,+∞)为增区间,综上,函数y的增区间为[1,+∞),正确;
④因为1+log34<3,所以f(1+log34)=f(1+1+log34),而2+log34>3,所以f(2+log34)=
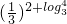 =
= ×
× =
= ,命题正确.
,命题正确.所以正确命题的序号是③④
故答案为:③④
点评:此题是一道综合题,要求学生掌握二次函数和对数函数的增减性,灵活运用对数函数的运算性质,会利用举反例的方法说明一个命题是假命题.

练习册系列答案
相关题目