网址:http://m.1010jiajiao.com/timu_id_33096[举报]
考 生 填 写 座 位
号 码 的 末 两 位
题 号
一
二
三
四
17
18
19
20
21
22
23
得 分
一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的;每小题选出答案后,请用2B铅笔把机读卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
C
A
B
A
C
D
D
C
D
得分
评卷人
二.填空题(请把答案填在对应题号的横线上)
13. . 14.
. 14. .
.
15. . 16.
. 16.  (或
(或 ) .
) .
三.解答题(本大题共5小题,共64分.解答应写出文字说明、证明过程或演算步骤.请将答题的过程写在答题卷中指定的位置.)
17.( 本题满分12分)
解:(Ⅰ)由递推关系 (2分)得,
(2分)得, (3分);
(3分); ;
; (6分),
(6分),
(Ⅱ)由 ,即
,即 (7分),所以
(7分),所以 ;.........12分(不单列
;.........12分(不单列 扣1分)
扣1分)
18.(本题满分12分)
 证明:(Ⅰ) 在三棱柱
证明:(Ⅰ) 在三棱柱 中,
中,
∵侧棱垂直底面 ,
,
∴ 四边形 ,
, ,
, 都是矩形,
都是矩形,
又 ∵  ,
, ,
, ,
,
∴  ,又 ∵
,又 ∵  为
为 中点,
中点,
在 中,
中, ,同理,
,同理, .
.
∴  ,∴
,∴  ,.....4分
,.....4分
在 中,
中, ,
,
在 中,
中, ,
,
∴  ,∴
,∴  .....6分
.....6分
又  ,
,
 ∴
∴  ...........8分
...........8分
(Ⅱ)由(Ⅰ)知 ,
,
∴ 直线 与平面
与平面 所成的角为
所成的角为 ...........9分
...........9分
在 中,
中,
∴  ,...............11分
,...............11分
即 直线 与平面
与平面 所成的角的余弦值为
所成的角的余弦值为 ........12分
........12分
解法二:(Ⅰ)以 为原点,建立如图所示的空间直角坐标系,设
为原点,建立如图所示的空间直角坐标系,设 ,
, ,
, ,
, (3分),则
(3分),则  ,
, ,
, ,
∴
,
∴  ,
,
∴ ,∴
,∴ (5分),
(5分),
∴  ,
,
∴  ,∴
,∴ (7分)
(7分)
又  ,∴
,∴  .....8分
.....8分
(Ⅱ)设向量 与
与 的夹角为
的夹角为 ,
,
∵ ,
,
∴

 ....10分
....10分
设直线 与平面
与平面 所成的角为
所成的角为
∵ 平面
平面
∴

∴直线 与平面
与平面 所成角的余弦值为
所成角的余弦值为 .…………………………12分
.…………………………12分
19.(本题满分12分)
解:(Ⅰ)每个提升站需要紧急维修的概率为 (2分),不需要紧急维修的概率为
(2分),不需要紧急维修的概率为 (3分),设需要维修的提升站数为
(3分),设需要维修的提升站数为 ,则
,则 .
.
 , (4分)
, (4分)
 , (5分)
, (5分)
 , (6分)
, (6分)
 .(7分)
.(7分)
(Ⅱ)∵ ,∴
,∴  的取值是
的取值是 ,则
,则 (元)的分布列是:
(元)的分布列是:










..................(9分)
∵ ,∴
,∴ ,又
,又  ,
,
∴  .
.
(或 )
)
答:紧急维修费用的数学期望是750元...........12分
20.(本题满分14分)
解: (Ⅰ)设“封闭函数 ”  的“封闭区间”为
的“封闭区间”为 ,其中
,其中 .
.

 在
在 上为减函数,故有:
上为减函数,故有: ,
,
解得: ,
, ,
,
∴  的“封闭区间”为
的“封闭区间”为 ..........4分
..........4分
(Ⅱ) ,令
,令 ,得:
,得: ....6分
....6分
∴  在(
在(
 ,0)上是增函数,在(2 ,+
,0)上是增函数,在(2 ,+ )上也是增函数;在(0 ,2)上是减函数.
)上也是增函数;在(0 ,2)上是减函数.
显然 在
在 上不是单调函数,故
上不是单调函数,故 不是
不是 上的“封闭函数 ”....8分
上的“封闭函数 ”....8分
(Ⅲ)假设存在实数 ,使函数
,使函数 是
是 上的“封闭函数 ”且“封闭区间”是
上的“封闭函数 ”且“封闭区间”是 ,则
,则
(1) 函数 在
在 上是单调函数.
上是单调函数.

 ,若函数
,若函数 在
在 上是增函数,则
上是增函数,则 对
对 恒成立,则:
恒成立,则:
 ;解得:
;解得: ....10分
....10分
(2) 由 ,知
,知 ,故函数
,故函数 在
在 上是增函数,所以, 函数
上是增函数,所以, 函数 在区间
在区间 上是增函数,故有:
上是增函数,故有:
 ,∵
,∵ ,∴
,∴ ,从而方程
,从而方程 至少有两个不相等的实数根.
至少有两个不相等的实数根.
又方程 有一根为
有一根为 ,故:方程
,故:方程 至少有一个不为
至少有一个不为 的根.
的根.
∴ ,解得:
,解得:

 且
且
 0..........13分
0..........13分
由(1),(2)知:3


 ...........14分
...........14分
21.(本题满分14分)
 解:(Ⅰ)∵离心率
解:(Ⅰ)∵离心率 ,且短半轴长
,且短半轴长 ,
,
∴  ,∴
,∴ ,
,
∴ 椭圆 的方程为
的方程为 ..............5分
..............5分
(Ⅱ)设 ,则
,则 ,
, ,则
,则 (6分),则直线
(6分),则直线 的方程为
的方程为 ,联立
,联立 ,得
,得
 (8分),
(8分),
(或写成: (8分),
(8分),
(或 ,即
,即  (8分)
(8分)
∵  ,∴
,∴  )
)
解之: ,
, (10分),
(10分),
∴  (11分),
(11分),
(或 ,
, (11分),)
(11分),)
又 ∵ 、
、 、
、 三点共线,∴
三点共线,∴  (12分),而
(12分),而  ,
,
∴  ,..............13分
,..............13分
(或 (13分),解之:
(13分),解之: ......14分)
......14分)
∵  ,∴
,∴  ,解之:
,解之: .........14分.
.........14分.
 四.选考题(从下列三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分; 请将答题的过程写在答题卷中指定的位置)
四.选考题(从下列三道解答题中任选一道作答,作答时,请注明题号;若多做,则按首做题计入总分,满分10分; 请将答题的过程写在答题卷中指定的位置)
你选做_______题(请在横线上注明题号)
解(或证明):
22.证明:∵ 是
是 的切线,直线
的切线,直线 是
是 的割线
的割线
∴  ,(2分)
,(2分)
又 ∵  ,∴
,∴  ,∴
,∴ (5分),
(5分),
∵  ,
,
∴ △ 与△
与△ 两边对应成比例,且夹角相等(7分),
两边对应成比例,且夹角相等(7分),
∴ △ ∽△
∽△ (8分)
(8分)
∴  (10分).
(10分).
23.解:(Ⅰ)直线 的参数方程是
的参数方程是 ,即
,即  ..5分
..5分
 (Ⅱ)设
(Ⅱ)设 ,则
,则 ,
,
∵ ,
, (7分),
(7分),
∴  ,即圆
,即圆 的极坐标方程为
的极坐标方程为
 ..........10分
..........10分
24.解:由 得
得  ,∴不等式的解集为
,∴不等式的解集为 (4分)
(4分)
∵
∴当 ≤1时,
≤1时, 为空集,显然成立,......6分
为空集,显然成立,......6分
当 >1时,
>1时, =
= ......8分
......8分
由 得
得  或
或
 或
或 ,即
,即 ,
,
这与 >1矛盾,
>1矛盾,
综合上述得: ≤1........10分
≤1........10分
(1)若定义域D1=(0,1),判断函数g(x)=2x-1是否在D1上封闭,并说明理由;
(2)若定义域D2=(1,5],是否存在实数a,使得函数f(x)=
| 5x-a | x+2 |
(3)利用(2)中函数,构造一个数列{xn},方法如下:对于给定的定义域D2=(1,5]中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述构造数列的过程中,如果xi(i=1,2,3,4…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个无穷常数列{xn},求实数a的取值范围.
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的取值范围.
给出函数封闭的定义:若对于定义域D内的任意一个自变量x0,都有函数值f(x0)∈D,称函数y=f(x)在D上封闭.
(1)若定义域D1=(0,1),判断函数g(x)=2x-1是否在D1上封闭,并说明理由;
(2)若定义域D2=(1,5],是否存在实数a,使得函数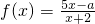 在D2上封闭?若存在,求出a的取值范围;若不存在,请说明理由.
在D2上封闭?若存在,求出a的取值范围;若不存在,请说明理由.
(3)利用(2)中函数,构造一个数列{xn},方法如下:对于给定的定义域D2=(1,5]中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述构造数列的过程中,如果xi(i=1,2,3,4…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个无穷常数列{xn},求实数a的取值范围.
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的取值范围.
查看习题详情和答案>>
(1)若定义域D1=(0,1),判断函数g(x)=2x-1是否在D1上封闭,并说明理由;
(2)若定义域D2=(1,5],是否存在实数a,使得函数f(x)=
| 5x-a |
| x+2 |
(3)利用(2)中函数,构造一个数列{xn},方法如下:对于给定的定义域D2=(1,5]中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述构造数列的过程中,如果xi(i=1,2,3,4…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个无穷常数列{xn},求实数a的取值范围.
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的取值范围.