题目内容
给出函数封闭的定义:若对于定义域D内的任意一个自变量x0,都有函数值f(x0)∈D,称函数y=f(x)在D上封闭.
(1)若定义域D1=(0,1),判断函数g(x)=2x-1是否在D1上封闭,并说明理由;
(2)若定义域D2=(1,5],是否存在实数a,使得函数f(x)=
在D2上封闭?若存在,求出a的取值范围;若不存在,请说明理由.
(3)利用(2)中函数,构造一个数列{xn},方法如下:对于给定的定义域D2=(1,5]中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述构造数列的过程中,如果xi(i=1,2,3,4…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个无穷常数列{xn},求实数a的取值范围.
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的取值范围.
(1)若定义域D1=(0,1),判断函数g(x)=2x-1是否在D1上封闭,并说明理由;
(2)若定义域D2=(1,5],是否存在实数a,使得函数f(x)=
| 5x-a |
| x+2 |
(3)利用(2)中函数,构造一个数列{xn},方法如下:对于给定的定义域D2=(1,5]中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述构造数列的过程中,如果xi(i=1,2,3,4…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个无穷常数列{xn},求实数a的取值范围.
②如果取定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的取值范围.
(1)对于定义域D内的任意一个自变量x0,都有函数值g(x0)∈(-1,1)∉D1,
故函数g(x)=2x-1在D1上不封闭;
(2)若存在,则f(x)=
=5-
,
∵定义域D2=(1,5],∴(
,
]∈(1,5],
∴-10≤a≤-2
(3)①根据题意,只需当x≠-2时,方程f(x)=x有解,方程x2-3x+a=0有不等于2的解.
将x=-2代入方程,得a=-10,由此可得a的取值范围是(-∞,-10)∪(-10,+∞).
②根据题意,f(x)=
=a在R中无解,
亦即当x≠-2时,方程(5-a)x=3a无实数解.
∴a=5即为所求a的值.
故函数g(x)=2x-1在D1上不封闭;
(2)若存在,则f(x)=
| 5x-a |
| x+2 |
| 10+a |
| x+2 |
∵定义域D2=(1,5],∴(
| 5-a |
| 3 |
| 25-a |
| 7 |
∴-10≤a≤-2
(3)①根据题意,只需当x≠-2时,方程f(x)=x有解,方程x2-3x+a=0有不等于2的解.
将x=-2代入方程,得a=-10,由此可得a的取值范围是(-∞,-10)∪(-10,+∞).
②根据题意,f(x)=
| 5x-a |
| x+2 |
亦即当x≠-2时,方程(5-a)x=3a无实数解.
∴a=5即为所求a的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,都有函数值
,都有函数值 ,则称函数y=f(x)在 D上封闭。
,则称函数y=f(x)在 D上封闭。 判断下列函数中哪些在
判断下列函数中哪些在 上封闭,并给出推理过程;
上封闭,并给出推理过程;
 是否存在实数
是否存在实数 ,使函数
,使函数 在
在 上封闭,若存在,求出
上封闭,若存在,求出 -
- +1,f3(x)=2x-1;
+1,f3(x)=2x-1;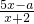 在D2上封闭?若存在,求出a的值,并给出证明;若不存在,请说明理由.
在D2上封闭?若存在,求出a的值,并给出证明;若不存在,请说明理由.