网址:http://m.1010jiajiao.com/timu_id_330328[举报]
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
A
B
C
D
C
D
二、填空题
13.2 14. 15.60 16.③④
15.60 16.③④
三、解答题
17.解:(1) ,
,
 (2分)
(2分)
又 (4分)
(4分)
 . (6分)
. (6分)
(2)
 (8分)
(8分)

 (10分)
(10分)
18.(1)证明:连结 交
交 于点
于点 ,取
,取 的中点
的中点 ,连结
,连结 ,则
,则 //
// 
 且
且 依题意,知
依题意,知 且
且 ,
,
 ,且
,且 ,
,
故四边形 是平行四边形,
是平行四边形,
 ,即
,即 (4分)
(4分)
又 平面
平面 ,
,

 平面
平面 , (6分)
, (6分)
(2)延长 交
交 的延长线于
的延长线于 点,连结
点,连结 ,作
,作 于
于 点,连结
点,连结 .
.
∵平面 平面
平面 ,平面
,平面 平面
平面 ,
,
 平面
平面 ,
,
∴ 平面
平面 ,
,
由三垂线定理,知 ,故
,故 就是所求二面角的平面角.(8分)
就是所求二面角的平面角.(8分)
∵平面 平面
平面 ,平面
,平面 平面
平面
 平面
平面 ,故
,故 就是直线
就是直线 与平面
与平面 成的角, (10分)
成的角, (10分)
知 设
设 ,则
,则 .
.
在 中:
中:

在 中:由
中:由 ,
, ,知
,知
故平面 与平面
与平面 所成的锐二面角的大小为45°. (12分)
所成的锐二面角的大小为45°. (12分)
19.解:(1)记 表示事无偿援助,“取出的2伯产吕中无二等品”,
表示事无偿援助,“取出的2伯产吕中无二等品”, 表示事件“取出的2件产品中恰有1件是二等品”。则
表示事件“取出的2件产品中恰有1件是二等品”。则 、
、 互斥,且
互斥,且
故
依题意,知 又
又 ,得
,得 (6分)
(6分)
(2)若该批产品有100件,由(1)知,其中共有二等品100×0.2=20件
记 表示事件“取出的2件产品中无二等品”,则事件
表示事件“取出的2件产品中无二等品”,则事件 与事件
与事件 互斥,
互斥,
依题意,知
故 (12分)
(12分)
20.解:(1) 在
在 上单调递增,
上单调递增, 上单调递减,
上单调递减,
 有两根
有两根 ,2,
,2,
 (6分)
(6分)
(2)令 则
则
因为 在
在 上恒大于0,
上恒大于0,
所以 ,在
,在 上单调递增,故
上单调递增,故
 (12分)
(12分)
21.(1)依题意,知
由 ,得
,得
故 ,得
,得 4分
4分
(2)依题意,知
由 ,得
,得
即 ,得
,得 8分
8分
(3)由 、
、 是相互垂直的单位向量,
是相互垂直的单位向量, 知,
知,
得
记数列 的前
的前 项和为
项和为 ,
,
则有

相减得,
故 12分
12分
22.解:(1)设 依题意得
依题意得
 (2分)
(2分)
消去 ,
, ,整理得
,整理得 . (4分)
. (4分)
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示圆. (6分)
时,方程表示圆. (6分)
(2)当 时,方程为
时,方程为 设直线
设直线 的方程为
的方程为
 (8分)
(8分)
消去 得
得 (10分)
(10分)
根据已知可得 ,故有
,故有
 直线
直线 的斜率为
的斜率为 (12分)
(12分)
 若椭圆E1:
若椭圆E1:| x2 | ||
|
| y2 | ||
|
| x2 | ||
|
| y2 | ||
|
| a2 |
| a1 |
| b2 |
| b1 |
|
(1)求经过点(2,
| 6 |
| x2 |
| 4 |
| y2 |
| 2 |
(2)设过原点的一条射线l分别与(1)中的两个椭圆交于A、B两点(其中点A在线段OB上),
求|OA|+
| 1 |
| |OB| |
(3)对于真命题“过原点的一条射线分别与相似比为2的两个椭圆C1:
| x2 |
| 22 |
| y2 | ||
(
|
| x2 |
| 42 |
| y2 | ||
(2
|
| x2 |
| 32 |
| y2 | ||||
(
|
假设一个人从出生到死亡,在每个生日都测量身高,并作出这些数据散点图,则这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析.下表是一位母亲给儿子作的成长记录:
| 年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 90.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| 年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.6 | 173.0 |
(1)作出这些数据的散点图;
(2)求出这些数据的回归方程;
(3)对于这个例子,你如何解释回归系数的含义?
(4)用下一年的身高减去当年的身高,计算他每年身高的增长数,并计算他从3~16岁身高的年均增长数.
(5)解释一下回归系数与每年平均增长的身高之间的联系.
查看习题详情和答案>>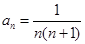 ,数列
,数列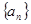 的前
的前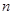 项的和记为
项的和记为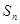 .
.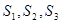 的值,猜想
的值,猜想