摘要：结论 问题:
网址：http://m.1010jiajiao.com/timu_id_327[举报]
一、选择题:1. A 2.C 3.B 4.B 5.C 6.B 7.B 8.D 9.C 10.D
二、填空题:1. 1.5×108 2. 短
3. y=.files/image045.gif)
4..files/image047.gif)
,
5.
5cm 6. 瑞士 7. xn+1 -1 8. .files/image049.gif)
9. 一 10.n
三、
1、（2a+1）2-(2a+1)(2a-1)=4a2+4a+1-4a2+1=4a+2,
当a=.files/image031.gif)
时,.files/image052.gif)
2 、(1)作AC的垂直平分线MN，与AC交于O点，与BE延长线交点为求作点D。
(2)有外接圆
连结AD、CD，过D点作DE、DF分别垂直于AB、CB。
由△EDA≌△FDC得OA=OB=OC=OD,.files/image054.gif)
=25.
四、设鸡场的一边为xcm,另外两边均为.files/image056.gif)
cm,
x×=180, x1=20+2.files/image058.gif)
, x2=20-2,能达180m2.
当x×=200,x1= x2=20,能达到200m2 ;
当x×=250,方程无解,不能达到.
五、多种方式，合理即可.
六、结论（与统计知识有关即可，至少写3个）
(1)条形，（能清楚地表示出每个项目的具体数目
(2)能清楚地反映事物的变化情况
(3)能清楚地表示出各部分在总体中所占的百分比
七、(1）（24+23+……+24）÷9=24
一天：24×24×60=34560
(2).files/image061.gif)
(3) 700000+100×3×365=
x≈1.8（倍.毛
问题探索：
（1）已知一个正分数
（m＞n＞0），如果分子、分母同时增加1，分数的值是增大还是减小？请证明你的结论．
（2）若正分数
（m＞n＞0）中分子和分母同时增加2，3…k（整数k＞0），情况如何？
（3）请你用上面的结论解释下面的问题：
建筑学规定：民用住宅窗户面积必须小于地板面积，但按采光标准，窗户面积与地板面积的比应不小于10%，并且这个比值越大，住宅的采光条件越好，问同时增加相等的窗户面积和地板面积，住宅的采光条件是变好还是变坏？请说明理由． 查看习题详情和答案>>
（1）已知一个正分数
| n |
| m |
（2）若正分数
| n |
| m |
（3）请你用上面的结论解释下面的问题：
建筑学规定：民用住宅窗户面积必须小于地板面积，但按采光标准，窗户面积与地板面积的比应不小于10%，并且这个比值越大，住宅的采光条件越好，问同时增加相等的窗户面积和地板面积，住宅的采光条件是变好还是变坏？请说明理由． 查看习题详情和答案>>
22、问题：你能比较两个数20022003与20032002的大小吗？为了解决这个问题，我们先把它抽象成这样的问题：写成它的一般形式，即比较nn+1和（n+1）n的大小（n是自然数）．然后，我们分析n=1，n=2，n=3…这些简单情形入手，从而发现规律，经过归纳，才想出结论．
（1）通过计算，比较下列各组中两个数的大小（在空格中填“＜”“＞”“=”）
①12＜21②23＜32③34＞43④45＞54
⑤56＞65⑥66＞75
（2）从第（1）题的结果经过归纳，可以猜想出nn+1和（n+1）n的大小关系；
（3）根据上面归纳猜想得到的一般结论，试比较下列两个数的大小：20022003＞20032002．
查看习题详情和答案>>
（1）通过计算，比较下列各组中两个数的大小（在空格中填“＜”“＞”“=”）
①12＜21②23＜32③34＞43④45＞54
⑤56＞65⑥66＞75
（2）从第（1）题的结果经过归纳，可以猜想出nn+1和（n+1）n的大小关系；
（3）根据上面归纳猜想得到的一般结论，试比较下列两个数的大小：20022003＞20032002．
问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
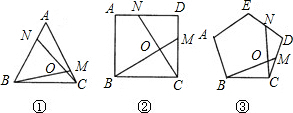
①如图1，在正三角形ABC中，M，N分别是AC，AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN；
②如图2，在正方形ABCD中，M，N分别是CD，AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
然后运用类比的思想提出了如下命题；
③如图3，在正五边形ABCDE中，M，N分别是CD，DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN．任务要求：
（1）请你从①，②，③三个命题中选择一个进行证明；
（2）请你继续完成下面的探索：
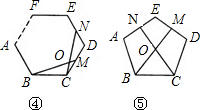
①如图4，在正n（n≥3）边形ABCDEF…中，M，N分别是CD，DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM=CN成立；（不要求证明）
②如图5，在正五边形ABCDE中，M，N分别是DE，AE上的点，BM与CN相交于点O，若∠BON=108°时，试问结论BM=CN是否还成立．若成立，请给予证明；若不成立，请说明理由． 查看习题详情和答案>>
①如图1，在正三角形ABC中，M，N分别是AC，AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN；
②如图2，在正方形ABCD中，M，N分别是CD，AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
然后运用类比的思想提出了如下命题；
③如图3，在正五边形ABCDE中，M，N分别是CD，DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN．任务要求：
（1）请你从①，②，③三个命题中选择一个进行证明；
（2）请你继续完成下面的探索：
①如图4，在正n（n≥3）边形ABCDEF…中，M，N分别是CD，DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM=CN成立；（不要求证明）
②如图5，在正五边形ABCDE中，M，N分别是DE，AE上的点，BM与CN相交于点O，若∠BON=108°时，试问结论BM=CN是否还成立．若成立，请给予证明；若不成立，请说明理由． 查看习题详情和答案>>
