如图所示，表示五个共点力的有向线段恰分别构成正六边形的两条邻边和三条对角线．已知F₁＝10N，这五个共点力的合力大小为(　　)

图2－5－13

A．0                                 B．30 N

C．60 N                              D．90 N

【解析】：选C.先把F₁、F₄合成，则F₁₄＝F₃，再把F₂、F₅合成，则F₂₅＝F₃，由几何关系可知F₃＝2F₁＝20 N，所以F_合＝3F₃＝60 N.

如图所示，表示五个共点力的有向线段恰分别构成正六边形的两条邻边和三条对角线．已知F₁＝10 N，这五个共点力的合力大小为(　　)

图2－5－13

A．0                                 B．30 N

C．60 N                              D．90 N

【解析】：选C.先把F₁、F₄合成，则F₁₄＝F₃，再把F₂、F₅合成，则F₂₅＝F₃，由几何关系可知F₃＝2F₁＝20 N，所以F_合＝3F₃＝60 N.

如图，一透明球体置于空气中，球半径R＝10 cm，折射率n＝.MN是一条通过球心O的直线，单色细光束AB平行于MN射向球体，AB与MN间距为5 cm，CD为出射光线．

(1)补全光路并求出光从B点传到C点的时间；

(2)求CD与MN所成的角α.(需写出求解过程)

【解析】：(1)连接BC，如图18

在B点光线的入射角、折射角分别标为i、r

sini＝5/10＝，所以，i＝45°

由折射率定律：在B点有：n＝　sinr＝1/2

故：r＝30°　＝2Rcosr

t＝n/c＝2Rncosr/c

t＝(/3)×10^－9 s

(2)由几何关系可知∠COP＝15°

∠OCP＝135°　α＝30°

(10分)如图所示，质量分布不均匀的直细杆AB长1 m，将它的两端用两根细绳拴住吊在两竖直墙上，当AB在水平方向平衡时，细绳AC与竖直方向的夹角为θ₁＝60°，细绳BD与竖直方向的夹角为θ₂＝30°.求AB杆的重心距B端的距离．

图4－18

【解析】：以AB杆为研究对象，受力分析如图所示，AC绳的拉力为F₁，BD绳的拉力为F₂.F₁、F₂的作用线交于E点，则重力G的作用线必过E点．过E点作竖直线交AB杆于O点，O点即为AB杆重心的位置．

由几何关系可知

＝·sin30°＝·sin30°·sin30°

＝＝0.25 m.

即细杆的重心距B端0.25 m.

如图，一透明球体置于空气中，球半径R＝10 cm，折射率n＝.MN是一条通过球心O的直线，单色细光束AB平行于MN射向球体，AB与MN间距为5 cm，CD为出射光线．

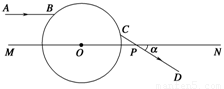
(1)补全光路并求出光从B点传到C点的时间；

(2)求CD与MN所成的角α.(需写出求解过程)

【解析】：(1)连接BC，如图18

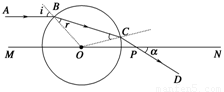
在B点光线的入射角、折射角分别标为i、r

sini＝5/10＝，所以，i＝45°

由折射率定律：在B点有：n＝　sinr＝1/2

故：r＝30°　＝2Rcosr

t＝n/c＝2Rncosr/c

t＝(/3)×10^－9 s

(2)由几何关系可知∠COP＝15°

∠OCP＝135°　α＝30°