摘要：18．解:依题意:张娟娟射击一次,击中10环的概率为.
网址：http://m.1010jiajiao.com/timu_id_323271[举报]
(理)甲与乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次数为f；乙用这枚硬币掷2次，记正面朝上的次数为η．
(1)分别求ξ和η的期望；
(2)规定：若ξ＞η，则甲获胜；若ξ＜η，则乙获胜，分别求出甲和乙获胜的概率．
(文)甲、乙两人各射击一次，击中目标的概率分别为
、
．假设每次射击是否击中目标相互之间没有影响，两人射击是否击中目标相互之间也没有影响．
(1)求甲连续射击4次，至少1次未击中目标的概率；
(2)求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；
(3)假设某人连续2次未击中目标，则中止射击．求乙恰好射击5次后，被中止射击的概率．
查看习题详情和答案>>
甲、乙、丙三名射击运动员射中目标的概率分别为
，a，a（0＜a＜1），三人各射击一次，击中目标的次数记为ξ．
（1）求ξ的分布列及数学期望；
（2）在概率P（ξ=i）（i=0，1，2，3）中，若P（ξ=1）的值最大，求实数a的取值范围． 查看习题详情和答案>>
| 1 | 2 |
（1）求ξ的分布列及数学期望；
（2）在概率P（ξ=i）（i=0，1，2，3）中，若P（ξ=1）的值最大，求实数a的取值范围． 查看习题详情和答案>>
甲、乙、丙三名射击运动员射中目标的概率分别为
，a，a（0＜a＜1），三人各射击一次，击中目标的次数记为ξ．
（1）求ξ的分布列及数学期望；
（2）在概率P（ξ=i）（i=0，1，2，3）中，若P（ξ=1）的值最大，求实数a的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
（1）求ξ的分布列及数学期望；
（2）在概率P（ξ=i）（i=0，1，2，3）中，若P（ξ=1）的值最大，求实数a的取值范围．
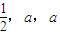（0＜a＜1），三人各射击一次，击中目标的次数记为ξ．