摘要:15.若为奇函数.且最大值为.则有序实数对是 .
网址:http://m.1010jiajiao.com/timu_id_3209636[举报]
已知函数f(x)=x3+ax2+bx+c,在定义域x∈[-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为-1.有以下命题:
①f(x)是奇函数;②若f(x)在[s,t]内递减,则|t-s|的最大值为4;③f(x)的最大值为M,最小值为m,则M+m=0; ④若对?x∈[-2,2],k≤f′(x)恒成立,则k的最大值为2.其中正确命题的序号为
查看习题详情和答案>>
①f(x)是奇函数;②若f(x)在[s,t]内递减,则|t-s|的最大值为4;③f(x)的最大值为M,最小值为m,则M+m=0; ④若对?x∈[-2,2],k≤f′(x)恒成立,则k的最大值为2.其中正确命题的序号为
①③
①③
.
已知函数f(x)=x3+ax2+bx+c,在定义域x∈[-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为-1.有以下命题:
①f(x)是奇函数;②若f(x)在[s,t]内递减,则|t-s|的最大值为4;③f(x)的最大值为M,最小值为m,则M+m=0; ④若对?x∈[-2,2],k≤f′(x)恒成立,则k的最大值为2.其中正确命题的序号为 . 查看习题详情和答案>>
①f(x)是奇函数;②若f(x)在[s,t]内递减,则|t-s|的最大值为4;③f(x)的最大值为M,最小值为m,则M+m=0; ④若对?x∈[-2,2],k≤f′(x)恒成立,则k的最大值为2.其中正确命题的序号为 . 查看习题详情和答案>>
已知函数 ,在定义域
,在定义域 [-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为
[-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为 .有以下命题:
.有以下命题:
① 是奇函数;②若
是奇函数;②若 在
在 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 ; ④若对
; ④若对 ,
,  恒成立,则
恒成立,则 的最大值为2.其中正确命题的序号为————
的最大值为2.其中正确命题的序号为————
查看习题详情和答案>>
 ,在定义域
,在定义域 [-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为
[-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为 .有以下命题:
.有以下命题: 是奇函数;②若
是奇函数;②若 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ ,最小值为
,最小值为 ,则
,则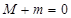 ; ④若对
; ④若对 ,
, 恒成立,则
恒成立,则 的最大值为2.其中正确命题的序号为————
的最大值为2.其中正确命题的序号为———— 既无最大值也无最小值;
既无最大值也无最小值;