题目内容
已知函数 ,在定义域
,在定义域 [-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为
[-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为 .有以下命题:
.有以下命题:
① 是奇函数;②若
是奇函数;②若 在
在 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 ; ④若对
; ④若对 ,
,  恒成立,则
恒成立,则 的最大值为2.其中正确命题的序号为————
的最大值为2.其中正确命题的序号为————
【答案】
①③
【解析】解:∵f(x)=x3+ax2+bx+c,在定义域x∈[-2,2]上表示的曲线过原点,∴f(0)=0∴c=0∵f′(x)=3x2+2ax+b,且在x=±1处的切线斜率均为-1.∴f′(1)=f′(-1)=-1
3+2a+b=-1和3-2a+b=-1,解可得b=-4,a=0∴f(x)=x3-4x,f′(x)=3x2-4
①∵f(-x)=-x3+4x=-f(x),即f(x)是奇函数;①正确
②由f′(x)≥0得单调区间进而得到结论。
③由奇函数的关于原点对称可知,最大值与最小值互为相反数,f(x)的最大值为M,最小值为m,则M+m=0;③正确
④若对∀x∈[-2,2],由于f′(x)=3x2-4∈[-4,8],则k≤f′(x)恒成立,则k≤4,则k的最大值为-4.④错误
正确命题的序号为①③

练习册系列答案
相关题目
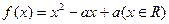 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在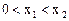 , 使得不等式
, 使得不等式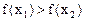 成立. 若
成立. 若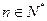 ,
,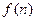 是数列
是数列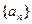 的前
的前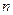 项和.
项和.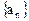 的通项公式;
的通项公式;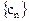 中,所有满足
中,所有满足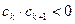 的正整数
的正整数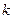 的个数称为这个数列
的个数称为这个数列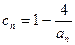 (n为正整数),求数列
(n为正整数),求数列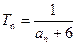 (
(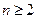 且
且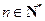 ),使不等式
),使不等式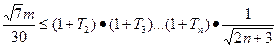 恒成立,求正整数
恒成立,求正整数 的最大值
的最大值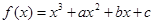 ,在定义域
,在定义域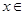 [-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为
[-2,2]上表示的曲线过原点,且在x=±1处的切线斜率均为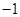 .有以下命题:
.有以下命题: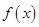 是奇函数;②若
是奇函数;②若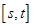 内递减,则
内递减,则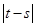 的最大值为4;③
的最大值为4;③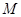 ,最小值为
,最小值为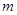 ,则
,则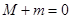 ;
④若对
;
④若对 ,
,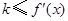 恒成立,则
恒成立,则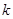 的最大
的最大 值为2.其中正确命题的个数为
值为2.其中正确命题的个数为 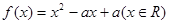 ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在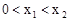 , 使得不等式
, 使得不等式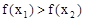 成立. 若
成立. 若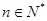 ,
,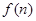 是数列
是数列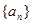 的前
的前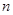 项和.
项和.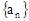 的通项公式;
的通项公式;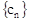 中,所有满足
中,所有满足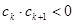 的正整数
的正整数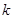 的个数称为这个数列
的个数称为这个数列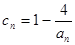 (n为正整数),求数列
(n为正整数),求数列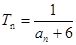 (
(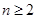 且
且 ),使不等式
),使不等式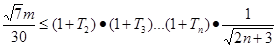 恒成立,求正整数
恒成立,求正整数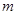 的最大值
的最大值