摘要: 已知等差数列}的公差大于0.且是方程的两根.数列}的前项和为.且 (Ⅰ)求数列}.}的通项公式, (Ⅱ)记.求数列中的最大项. 20. 如图.在四棱锥中.底面 是正方形.侧棱⊥底面..点是的中点, ⊥.且交于点. (Ⅰ)证明:∥平面, (Ⅱ)证明:⊥平面, (Ⅲ)求二面角的大小. .21. 已知椭圆的中心在坐标原点.焦点在轴上.它的一个顶点 恰好是抛物线的焦点.离心率为 (Ⅰ)求椭圆的标准方程, (Ⅱ)过椭圆的右焦点作直线交椭圆于.两点.交轴于点.若..求的值.
网址:http://m.1010jiajiao.com/timu_id_3206803[举报]
(本题满分14分) 已知等差数列 的公差
的公差 大于
大于 ,且
,且 、
、 是方程
是方程
 的两根.数列
的两根.数列 的前
的前 项和为
项和为 ,满足
,满足

(Ⅰ) 求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ) 设数列 的前
的前 项和为
项和为 ,记
,记 .若
.若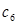 为数列
为数列 中的最大项,求实数
中的最大项,求实数 的取值范围.
的取值范围.
查看习题详情和答案>>
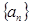 的公差
的公差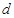 大于
大于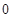 ,且
,且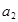 、
、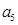 是方程
是方程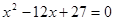 的两根.数列
的两根.数列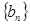 的前
的前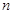 项和为
项和为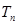 ,满足
,满足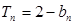
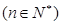

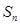 ,记
,记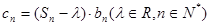 .若
.若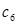 为数列
为数列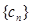 中的最大项,求实数
中的最大项,求实数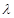 的取值范围.
的取值范围.  的前
的前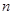 项和为
项和为 ,且
,且 .
. 满足
满足 ,求数列
,求数列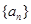 的前
的前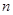 项和为
项和为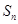 ,且
,且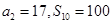 .
.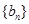 满足
满足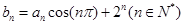 ,求数列
,求数列