摘要:..在单调递减--10分.--12分.所以.即的取值范围是--14分.
网址:http://m.1010jiajiao.com/timu_id_316113[举报]
设f(x)=
x3+mx2+nx.
(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)在单调递减区间的长度是正整数,试求m和n的值.(注:区间(a,b)的长度为b-a) 查看习题详情和答案>>
| 1 | 3 |
(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)在单调递减区间的长度是正整数,试求m和n的值.(注:区间(a,b)的长度为b-a) 查看习题详情和答案>>
已知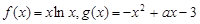
(1)求函数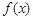 在
在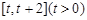 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有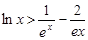 成立
成立
【解析】第一问中利用
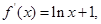 当
当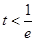 时,
时,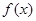 在
在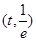 单调递减,在
单调递减,在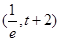 单调递增
单调递增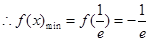 ,当
,当
 ,即
,即 时,
时,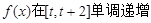 ,
,
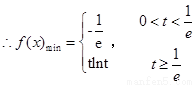
第二问中,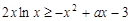 ,则
,则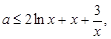 设
设 ,
,
则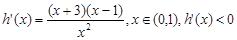 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,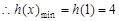 ,因为对一切
,因为对一切 ,
,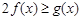 恒成立,
恒成立,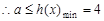
第三问中问题等价于证明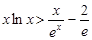 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则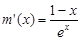 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)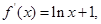 当
当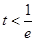 时,
时,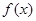 在
在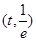 单调递减,在
单调递减,在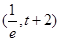 单调递增
单调递增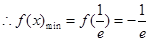 ,当
,当
 ,即
,即 时,
时,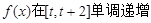 ,
,
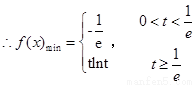 …………4分
…………4分
(2)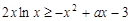 ,则
,则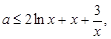 设
设 ,
,
则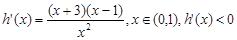 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,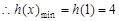 ,因为对一切
,因为对一切 ,
,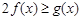 恒成立,
恒成立,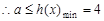 …………9分
…………9分
(3)问题等价于证明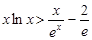 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则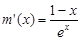 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
查看习题详情和答案>>
设f(x)= x3+mx2+nx.
x3+mx2+nx.
(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)在单调递减区间的长度是正整数,试求m和n的值.(注:区间(a,b)的长度为b-a)
查看习题详情和答案>>
 x3+mx2+nx.
x3+mx2+nx.(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)在单调递减区间的长度是正整数,试求m和n的值.(注:区间(a,b)的长度为b-a)
查看习题详情和答案>>
 x3+mx2+nx.
x3+mx2+nx. x3+mx2+nx.
x3+mx2+nx.