网址:http://m.1010jiajiao.com/timu_id_31495[举报]
一、不定项选择题(40分)
1
2
3
4
5
6
7
8
9
10
B
BD
BD
CD
D
A
C
BC
D
BD
二、实验题(20分)
11.(1)0.97 m/s (2)0.48 J 0.47 J
(3)重锤下落时受到空气阻力以及纸带受到打点计时器的阻力作用,重锤机械能减小.
12.(1)D
(2)弹簧的原长l0 第一步中的弹簧压缩后的长度l1 滑块的总位移s 第二步中静止状态下弹簧的长度l2
(3) 
三、计算题(90分)
13.解:设经过时间t,物体到达P点
?(1)xP=v0t,yP=(1/2)(F/m)t2,xP/yP=cot37°,
?联解得
?t=3s,x=30m,y=22.5m,坐标(30m,22.5m)
?(2)vy=(F/m)t=15m/s,
?∴v= m/s,
m/s,
?tanα=vy/v0=15/10=3/2,
?∴ α=arctan(3/2),α为v与水平方向的夹角.
14.(1)F=12N (2)μ=0.2
15.解:启动前N1=mg,
?升到某高度时 N2=(17/18)N1=(17/18)mg,
?对测试仪 N2-mg′=ma=m(g/2),
?∴ g′=(8/18)g=(4/9)g,
?GmM/R2=mg,GmM/(R+h)2=mg′,解得:h=(1/2)R.
16.解:由匀加速运动的公式 v2=v02+2as
?得物块沿斜面下滑的加速度为
?a=v2/2s=1.42/(2×1.4)=0.7m/s2,
由于a<gsinθ=5m/s2,
?可知物块受到摩擦力的作用.

?分析物块受力,它受3个力,如图3.对于沿斜面的方向和垂直于斜面的方向,由牛顿定律有
?mgsinθ-f1=ma,
?mgcosθ-N1=0,
?分析木楔受力,它受5个力作用,如图3所示.对于水平方向,由牛顿定律有
?f2+f1cosθ-N1sinθ=0,
?由此可解得地面的作用于木楔的摩擦力
?f2=mgcosθsinθ-(mgsinθ-ma)cosθ=macosθ=1×0.7×( /2)=0.61N
/2)=0.61N
?此力的方向与图中所设的一致(即:水平向左).
17.解:(1)开始A、B处于静止状态时,有
?kx0-(mA+mB)gsin30°=0, ①
?设施加F时,前一段时间A、B一起向上做匀加速运动,加速度为a,t=0.2s,A、B间相互作用力为零,对B有:
?kx-mBgsin30°=mBa, ②
?x-x0=(1/2)at2, ③
?解①、②、③得:
?a=5m/s2,x0=0.05m,x=0.15m,
?初始时刻F最小
?Fmin=(mA+mB)a=60N.
?t=0.2s时,F最大
?Fmax-mAgsin30°=mAa,
?Fmax=mA(gsin30°+a)=100N,
?(2)ΔEPA=mAgΔh=mAg(x-x0)sin30°=5J.
18.(1) (2)
(2)
如图,在一无限长的小车上,有质量分别为m1和m2的两个滑块(m1>m2)随车一起向右匀速运动,设两滑块与小车间的动摩擦因数均为μ,其它阻力不计,当车突然停止时,以下说法正确的是

A.若μ=0,两滑块一定相碰
B.若μ=0,两滑块一定不相碰
C.若μ≠0,两滑块一定相碰
D.若μ≠0,两滑块一定不相碰
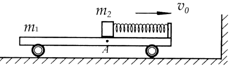 如图所示,在光滑水平地面上,有一质量m1=4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧.位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力.木块与A点左侧的车面之间的动摩擦因数μ=0.40,木块与A点右侧的车面之间的摩擦可忽略不计.现小车与木块一起以v0=2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v1=1.0m/s的速度反向弹回,已知重力加速度g取10m/s2,弹簧始终处于弹性限度内.求:
如图所示,在光滑水平地面上,有一质量m1=4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧.位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力.木块与A点左侧的车面之间的动摩擦因数μ=0.40,木块与A点右侧的车面之间的摩擦可忽略不计.现小车与木块一起以v0=2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v1=1.0m/s的速度反向弹回,已知重力加速度g取10m/s2,弹簧始终处于弹性限度内.求:(1)小车撞墙后弹簧的最大弹性势能;
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应满足什么条件?
如图所示,水平轻质弹簧与平板车A和物体B相连,将这三者视为一个系统放在光滑水平面上,处于静止状态,平板车A的质量为M,物体B的质量为m,且M>m.现用大小相等的水平恒力F1、F2拉A和B,从它们开始运动到弹簧第一次达到最长的过程中,(弹簧一直在弹性限度内,物体B不会离开平板车) ( ) 
| A.若物体与平板车之间也光滑,则系统动量守恒 |
| B.若物体与平板车之间也光滑,则系统机械能守恒 |
| C.无论物体与平板车有无摩擦,物体的最大动能大于平板车的最大动能 |
| D.弹簧第一次达到最长时A和B总动能最大 |
(1)求小车与竖直墙壁发生碰撞的过程中小车动量变化量的大小;
(2)若弹簧始终处于弹性限度内,求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能;
(3)要使木块最终不从小车上滑落,则车面A点左侧粗造部分的长度应满足什么条件?

如图11所示,在光滑水平地面上,有一质量m1=4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧。位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间的动摩擦因数μ=0.40,木块与A点右侧的车面之间的摩擦可忽略不计。现小车与木块一起以v0=2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v1=1.0m/s的速度水平向左运动,取g=10m/s2。
(1)求小车与竖直墙壁发生碰撞过程中小车动量变化量的大小;
(2)若弹簧始终处于弹性限度内,求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能;
(3)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应满足什么条件?
