摘要：由正弦定理得∴ .
网址：http://m.1010jiajiao.com/timu_id_314399[举报]
(理科)已知点H(－3，0)，点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足
，
．
(Ⅰ)当点P在y轴上移动时，求点M的轨迹C；
(Ⅱ)过定点D(m，0)(m＞0)作直线l交轨迹C于A、B两点，E是D点关于坐标原点
的对称点，求证：∠AED＝∠BED；
(Ⅲ)在(Ⅱ)中，是否存在垂直于x轴的直线
被以AD为直径的圆截得的弦长恒为定值？若存在求出的方程；若不存在，请说明理由．
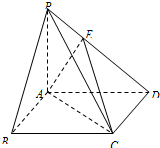如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，且PA=2，E点满足| PE |
| 1 |
| 3 |
| PD |
（1）证明：PA⊥平面ABCD；
（2）求二面角E-AC-D的余弦值．
（3）在线段BC上是否存在点F，使得PF∥平面EAC？若存在，确定点F的位置，若不存在请说明理由． 查看习题详情和答案>>
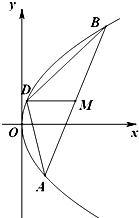如图，已知抛物线C：y2=2px（p＞0）上横坐标为4的点到焦点的距离为5．（Ⅰ）求抛物线C的方程；
（Ⅱ）设直线y=kx+b与抛物线C交于两点A（x1，y1），B（x2，y2），且|y1-y2|=a（a为正常数）．过弦AB的中点M作平行于x轴的直线交抛物线C于点D，连接AD、BD得到△ABD．
（i）求实数a，b，k满足的等量关系；
（ii）△ABD的面积是否为定值？若为定值，求出此定值；若不是定值，请说明理由．
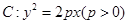上横坐标为4的点到焦点的距离为5．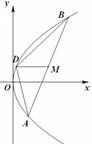
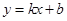与抛物线C交于两点
，
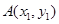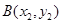，且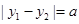
（a为正常数）．过弦AB的中点M作平行于x轴的直线交抛物线C于点D，连结AD、BD得到
．
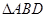上横坐标为4的点到焦点的距离为5．
与抛物线C交于两点
，
，且
（a为正常数）．过弦AB的中点M作平行于x轴的直线交抛物线C于点D，连结AD、BD得到
．