摘要:(1)求函数的“拐点 的坐标
网址:http://m.1010jiajiao.com/timu_id_314328[举报]
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f′′(x)是函数y=f(x)的导函数y=f′(x)的导数,若f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.现已知f(x)=x3-3x2+2x-2,请解答下列问题:
(Ⅰ)求函数f(x)的“拐点”A的坐标;
(Ⅱ)求证f(x)的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当x1>0,x2>0(x1≠x2)时,试比较
与G(
)的大小.
查看习题详情和答案>>
(Ⅰ)求函数f(x)的“拐点”A的坐标;
(Ⅱ)求证f(x)的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当x1>0,x2>0(x1≠x2)时,试比较
| G(x1)+G(x2) |
| 2 |
| x1+x2 |
| 2 |
对于三次函数f(x)=ax3+bx2+cx+d(a≠0)定义:设f′′(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x))为函数y=f(x)的“拐点”.已知函数f(x)=x3-6x2+5x+4,请回答下列问题.(1)求函数f(x)的“拐点”A的坐标
(2)检验函数f(x)的图象是否关于“拐点”A对称,对于任意的三次函数写出一个有关“拐点”的结论;
(3)写出一个三次函数G(x),使得它的“拐点”是(1,3)(不要过程) 查看习题详情和答案>>
(2)检验函数f(x)的图象是否关于“拐点”A对称,对于任意的三次函数写出一个有关“拐点”的结论;
(3)写出一个三次函数G(x),使得它的“拐点”是(1,3)(不要过程) 查看习题详情和答案>>
对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f′′(x)是函数y=f(x)的导函数y=f′(x)的导数,若f′′(x)=0有实数解x,则称点(x,f(x))为函数y=f(x)的“拐点”.现已知f(x)=x3-3x2+2x-2,请解答下列问题:
(Ⅰ)求函数f(x)的“拐点”A的坐标;
(Ⅱ)求证f(x)的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当x1>0,x2>0(x1≠x2)时,试比较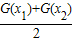 与
与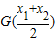 的大小.
的大小.
查看习题详情和答案>>
(Ⅰ)求函数f(x)的“拐点”A的坐标;
(Ⅱ)求证f(x)的图象关于“拐点”A 对称;并写出对于任意的三次函数都成立的有关“拐点”的一个结论(此结论不要求证明);
(Ⅲ)若另一个三次函数G(x)的“拐点”为B(0,1),且一次项系数为0,当x1>0,x2>0(x1≠x2)时,试比较
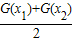 与
与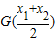 的大小.
的大小.查看习题详情和答案>>
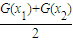 与
与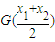 的大小.
的大小.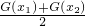 与
与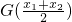 的大小.
的大小.