摘要：在N*是单调递增的.--------2分
网址：http://m.1010jiajiao.com/timu_id_30438[举报]
是定义在（0，+∞）上的单调递增函数，对于任意的m、n（m、n∈（0，+∞））满足
；
，解不等式
；(本小题满分12分) 已知函数
．
（1） 设F(x)=
在
上单调递增，求
的取值范围。
（2）若函数
与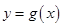
的图象有两个不同的交点M、N，求的取值范围；
（3）在（2）的条件下，过线段MN的中点作
轴的垂线分别与
的图像和
的图像交S、T点，以S为切点作的切线
，以T为切点作的切线
．是否存在实数使得
，如果存在，求出的值；如果不存在，请说明理由．
查看习题详情和答案>>
已知向量
=(
sin
，1)，
=(cos
，cos2
)，记f(x)=
•
，
（1）求f（x）的值域和单调递增区间；
（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足（2a-c）cosB=bcosC，若f(A)=
，试判断△ABC的形状．
查看习题详情和答案>>
| m |
| 3 |
| x |
| 4 |
| n |
| x |
| 4 |
| x |
| 4 |
| m |
| n |
（1）求f（x）的值域和单调递增区间；
（2）在△ABC中，角A、B、C的对边分别是a、b、c，且满足（2a-c）cosB=bcosC，若f(A)=
1+
| ||
| 2 |
，函数f(x)＝(m＋n)·m.
，c＝4，且f(A)是函数f(x)在
上的最大值，求△ABC的面积S.