网址：http://m.1010jiajiao.com/timu_id_29671[举报]
一、BCACB CBADD
二、11. a4 12. (1)
17. 如果AB=AD，BC=DC，那么∠ACB=∠ACD（或如果∠ACB=∠ACD，BC=DC，那么AB=AD）
18. 2
三、19．（1）原式
………………………………（3分）
………………………………（4分）
………………………………（5分）
当
时，原式
………………………………（8分）
20．（1）方程两边都乘以(x+1)(x-1)，约去分母，得 x-1=-2 …………（2分）
解这个整式方程，得 x=-1 ………………………………（4分）
检验: 把x=-1代入(x+1)(x-1)，得(x+1)(x-1)=0，
因此，x=-1不是原分式方程的根，所以原分式方程无解. ………（5分）
（2）原方程整理，得 x2-2x=2 …………………………（1分）
(x-1)2=3 …………………………（3分）
x-1=±
…………………………（4分）
∴ x1=1+, x2=1- …………………………（5分）
21．（1）这8天该类饮料平均日销售量是
(2×31+2×33+29+32+25+26)=30(箱) …………………………（4分）
（2）估计上半年该店能销售这类饮料181×30=5430（箱） …………（8分）
22．设原价为1个单位，每次提价的百分率为x. ………………………（1分）
根据题意，得
(1+x)2=
………………………………（4分）
解这个方程，得
（舍去） ………………（6分）
取
.
………………………………（7分）
答：每次提价的百分率约为22.5%. ………………………………（8分）
23. 证明：∵ OA=OB，
∴ ∠A=∠B. ……………………………（3分）
又 ∵ AC=BD,
∴ △OAC≌△OBD, ………………………………（7分）
∴ OC=OD, ………………………………（9分）
∴ ∠1=∠2. ………………………………（10分）
注：本题证法不唯一，其它证法可参照上述步骤给分.
24．（1）∵ 四边形ABCD和DCEF都是正方形，
∴ CD=DF，∠DCG=∠DFH=∠FDC=90°. ……………………………（2分）
∵ ∠CDG+∠CDH=∠CDH+∠FDH=90°,
∴ ∠CDG=∠FDH, ………………………………（4分）
∴ △CDG≌△FDH, ………………………………（5分）
∴ CG=FH. ………………………………（6分）
∵ BC=EF,
∴ BG=EH. ………………………………（8分）
（2）结论BG=EH仍然成立. ………………………………（9分）
同理可证△CDG≌△FDH. ………………………………（10分）
∴ CG=FH,
∵ BC=EF,
∴ BG=EH. ………………………………（12分）
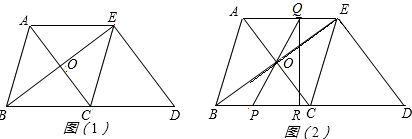
（1）判断四边形ABCE是怎样的四边形，说明理由；
（2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R．四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积．
查看习题详情和答案>>
| CB |
| AC |
| AC |
| AB |
| ||
| 2 |
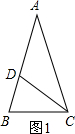
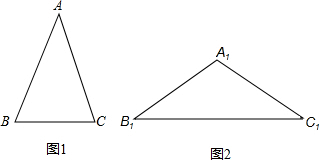
（1）如图1，在△ABC中，∠A=36°，AB=AC，∠ACB的角平分线CD交腰AB于点D，请你说明D为腰AB的黄金分割点的理由．
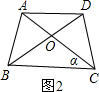
（2）若腰和上底相等，对角线和下底相等的等腰梯形叫作黄金梯形，其对角线的交点为对角线的黄金分割点．如图2，AD‖BC，AB=AD=DC，AC=BD=BC，试说明O为AC的黄金分割点．
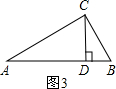
（3）如图3，在Rt△ABC中，∠ACB=90°，CD为斜边AB上的高，∠A、∠B、∠ACB的对边分别为a、b、c．若D是AB的黄金分割点，那么a、b、c之间的数量关系是什么并证明你的结论．
查看习题详情和答案>>
探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，分析发现∠BOC=90°+
| 1 |
| 2 |
∵BO和CO分别是∠ABC，∠ACB的角平分线
∴∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-（∠1+∠2）=180°-（90°-
| 1 |
| 2 |
| 1 |
| 2 |
（1）探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．
（2）探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（直接写出结论）
（3）拓展：如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）
（4）运用：如图5，五边形ABCDE中，∠BCD、∠EDC的外角分别是∠FCD、∠GDC，CP、DP分别平分∠FCD和∠GDC且相交于点P，若∠A=140°，∠B=120°，∠E=90°，则∠CPD=
（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；
（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；
（3）设
| BC |
| AC |
（4）如图2，在△A1B1C1中，已知A1B1=A1C1，∠A1=108°，且A1B1=AB，请直接写出
| BC |
| B1C1 |
查看习题详情和答案>>
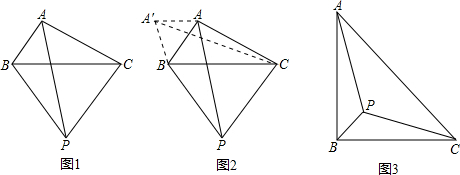
小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．
小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．
请你回答：AP的最大值是
参考小伟同学思考问题的方法，解决下列问题：
如图3，等腰Rt△ABC．边AB=4，P为△ABC内部一点，则AP+BP+CP的最小值是
| 2 |
| 6 |
32+16
|
| 2 |
| 6 |
32+16
|
