题目内容
如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE、AC和BE相交于点O.(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积.
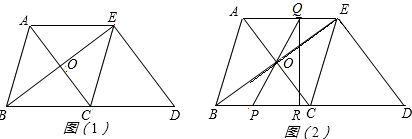
分析:(1)利用平移的知识可得四边形ABCE是平行四边形,进而根据AB=BC可得该四边形为菱形;
(2)利用证明三角形全等可得四边形PQED的面积为三角形BED的面积,所以不会改变;进而利用三角形的面积公式求解即可.
(2)利用证明三角形全等可得四边形PQED的面积为三角形BED的面积,所以不会改变;进而利用三角形的面积公式求解即可.
解答:解:(1)四边形ABCE是菱形,证明如下:
∵△ECD是由△ABC沿BC平移得到的,
∴EC∥AB,且EC=AB,
∴四边形ABCE是平行四边形,(2分)
又∵AB=BC,
∴四边形ABCE是菱形.(4分)
(2)由菱形的对称性知,△PBO≌△QEO,
∴S△PBO=S△QEO(7分)
∵△ECD是由△ABC平移得到的,
∴ED∥AC,ED=AC=6,
又∵BE⊥AC,∴BE⊥ED,(8分)
∴S四边形PQED=S△QEO+S四边形POED=S△PBO+S四边形POED=S△BED
=
×BE×ED=
×8×6=24.(10分)
∵△ECD是由△ABC沿BC平移得到的,
∴EC∥AB,且EC=AB,
∴四边形ABCE是平行四边形,(2分)
又∵AB=BC,
∴四边形ABCE是菱形.(4分)
(2)由菱形的对称性知,△PBO≌△QEO,
∴S△PBO=S△QEO(7分)
∵△ECD是由△ABC平移得到的,
∴ED∥AC,ED=AC=6,
又∵BE⊥AC,∴BE⊥ED,(8分)
∴S四边形PQED=S△QEO+S四边形POED=S△PBO+S四边形POED=S△BED
=
| 1 |
| 2 |
| 1 |
| 2 |
点评:考查菱形的判定及相关性质;把不规则图形的面积转化为较简单的规则图形的面积是解决本题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目

 明理由.
明理由.
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=