网址:http://m.1010jiajiao.com/timu_id_28577[举报]
一、选择题:本大题共10个小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
B
A
D
B
A
二、填空题:本大题共4个小题,每小题4分,共16分.
11. 630 12. 2k 13.  14. ①②③
14. ①②③
三、解答题:本大题共6个小题,每小题14分,共84分.
15. (4分)
(4分) 
由题意得

16.  有分布列:
有分布列:

0
1
2
3
P




从而期望
17.(1)
又

(2) 


(3)DE//AB,
(4)设BB1的中点为F,连接EF、DF,则EF是DF在平面BB
因为BB

18.(1) 由题意得

(2) 
所以直线 的斜率为
的斜率为
令 ,则直线
,则直线 的斜率
的斜率 ,
,
19.(1)由韦达定理得


 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
(2)由(1)知 ,则
,则
原式左边=
= =右式。故原式成立。
=右式。故原式成立。
20.令x=y=0,有 ,令y=-x则
,令y=-x则 得
得
故(1)得证。
(2)在R上任取x1,x2且 ,且
,且 ,
,

所以 在R上单调递增;
在R上单调递增;
(3)
由
 得
得 ;
;
由 得
得 ;因为
;因为 ,
,
所以 无解,即圆心到直线的距离大于或等于半径2,只需
无解,即圆心到直线的距离大于或等于半径2,只需

已知数列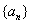 是等比数列,
是等比数列,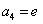 ,如果
,如果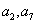 是关于
是关于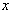 的方程:
的方程: 的两个实根,(
的两个实根,(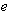 是自然对数的底数)
是自然对数的底数)
(1)求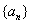 的通项公式;
的通项公式;
(2)设: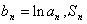 是数列
是数列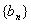 的前
的前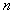 项的和,当
项的和,当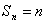 时,求
时,求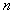 的值;
的值;
(3)对于(Ⅱ)中的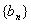 ,设
,设 ,而
,而 是数列
是数列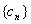 的前项的和,求
的前项的和,求 的最大值,及相应的
的最大值,及相应的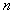 的值。
的值。
查看习题详情和答案>>
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
【解析】第一问中设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为
第二问中,设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得 
∵ ,∴
,∴
确定结论直线 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 得到。
得到。
(1)设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 ,
………………9分
,
………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 总能被
总能被 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
查看习题详情和答案>>
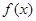 在定义域内存在区间
在定义域内存在区间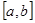 ,满足
,满足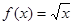 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出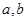 ;若不是,说明理由;
;若不是,说明理由;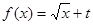 为“优美函数”,求实数
为“优美函数”,求实数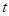 的取值范围.
的取值范围.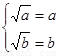 ,由
,由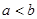 ,所以
,所以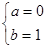
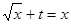 有两实根
有两实根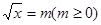 所以关于m的方程
所以关于m的方程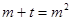 在
在 有两实根,
有两实根,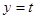 与函数
与函数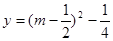 的图像在
的图像在