题目内容
已知数列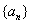 是等比数列,
是等比数列,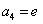 ,如果
,如果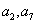 是关于
是关于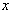 的方程:
的方程: 的两个实根,(
的两个实根,(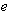 是自然对数的底数)
是自然对数的底数)
(1)求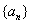 的通项公式;
的通项公式;
(2)设: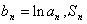 是数列
是数列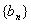 的前
的前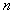 项的和,当
项的和,当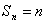 时,求
时,求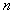 的值;
的值;
(3)对于(Ⅱ)中的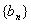 ,设
,设 ,而
,而 是数列
是数列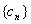 的前项的和,求
的前项的和,求 的最大值,及相应的
的最大值,及相应的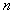 的值。
的值。
【答案】
解析:(I)由于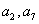 是已知方程的两根,所以有:
是已知方程的两根,所以有: ,即
,即 ,--------1分
,--------1分
而: 得
得 两式联立得:
两式联立得: -------------------------------------------------------2分
-------------------------------------------------------2分
所以 故得数列
故得数列 的通项公式为:
的通项公式为:
 .-------------------------------------------------------------------4分
.-------------------------------------------------------------------4分
(Ⅱ) =
= ,所以数列
,所以数列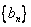 是等差数列,由前
是等差数列,由前 项和公式得:
项和公式得: ,得
,得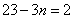 ,所以有
,所以有 .-------------------------------------7分
.-------------------------------------7分
(Ⅲ)由于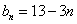 得:
得: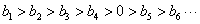 又因为
又因为 所以有:
所以有: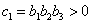 ,
, 而
而  ,
,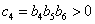 ,
, 且当
且当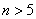 时都有
时都有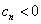 ,但是,
,但是, ,
,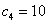 即:
即: 所以只有当
所以只有当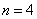 时,
时,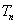 的值最大,此时
的值最大,此时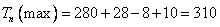 --------------------------------------12分
--------------------------------------12分

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 是等比数列,
是等比数列, 是等差数列,且
是等差数列,且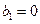 ,数列
,数列 满足
满足 ,其前四项依次为1,
,其前四项依次为1, ,
, ,2,求数列
,2,求数列 。
。 是等比数列,数列
是等比数列,数列 是等差数列,则
是等差数列,则 的值为 _____
的值为 _____ 是等比数列,且
是等比数列,且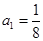 ,
, ,则
,则 为( )
为( ) C.2 D.
C.2 D. 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25. +
+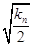 ,Sn=b12+b22+b32+…+
bn2, Tn=
,Sn=b12+b22+b32+…+
bn2, Tn= 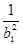 +
+ +
+ +…+
+…+ ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。 是等比数列,且
是等比数列,且 ,
,
 的表达式;
的表达式;  .
.