网址:http://m.1010jiajiao.com/timu_id_28532[举报]
一、选择题:(本题每小题5分,共50分)
1
2
3
4
5
6
7
8
9
10
D
B
C
D
D
C
B
A
A
C
二、填空题:(本题每小题4分,共16分)
11. 12.
12. 13.
13. 14.
14.
三、解答题(本大题6小题,共84分。解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分14分)
解 得
得 …………………4分
…………………4分
又

∵
 +1>
+1> 得B={y|y<
得B={y|y< 或y>
或y>
 +1}……………………8分
+1}……………………8分
∵A∩B=φ
 ∴
∴ 
 1
1

 +1
+1 9…………………12分
9…………………12分
∴
 -2
-2 …………………14分
…………………14分
16.(本小题满分14分)
解:(1) ,
,
由 得
得 又
又
 ………6分
………6分
(2)因

 ………8分
………8分
又 ,
, ,则
,则
即 …………………10分
…………………10分

 …14分
…14分
17.(本小题满分14分)
解: (…………………3分)
(…………………3分)
 =
= (…………………7分)
(…………………7分)
又 ,
, ,
,
(1)若 ,即
,即 时,
时, =
= =
= ,(…………10分)
,(…………10分)
(2)若 ,即
,即
 时,
时,
所以当 即
即 时,
时, =
= (…………………13分)
(…………………13分)
 (…………………14分)
(…………………14分)
18.(本小题满分14分)
解:(1)令 ,
, ,即
,即
由

∵ ,∴
,∴ ,即数列
,即数列 是以
是以 为首项、
为首项、 为公差的等差数列, ∴
为公差的等差数列, ∴ …………8分
…………8分
(2) 化简得
化简得 ,即
,即
∵ ,又∵
,又∵ 时,
时, …………12分
…………12分
∴各项中最大项的值为 …………14分
…………14分
19.(本小题满分14分)
解:(1) ,由题意
,由题意 ―――①
―――①
又 ―――②
―――②
联立得 …………5分
…………5分
(2)依题意得 即
即 ,对
,对 恒成立,设
恒成立,设 ,则
,则
解 得
得
当  ……10分
……10分
则
又 ,所以
,所以 ;故只须
;故只须  …………12分
…………12分
解得
即 的取值范围是
的取值范围是 …………14分
…………14分
20.(本小题满分14分)
解:(1)由 ,
,
 即函数
即函数 的图象交于不同的两点A,B; ……4分(2)
的图象交于不同的两点A,B; ……4分(2)
已知函数 ,
, 的对称轴为
的对称轴为 ,
,
故 在[2,3]上为增函数,
……………6分
在[2,3]上为增函数,
……………6分
 ……8分
……8分
(3)设方程
 ……10分
……10分
 ……12分
……12分
设 的对称轴为
的对称轴为 上是减函数,
上是减函数, ……14分
……14分
己知在锐角ΔABC中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]()
(I )求角![]() 大小;
大小;
(II)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.

20.如图1,在平面内,![]() 是
是![]() 的矩形,
的矩形,![]() 是正三角形,将
是正三角形,将![]() 沿
沿![]() 折起,使
折起,使![]() 如图2,
如图2,![]() 为
为![]() 的中点,设直线
的中点,设直线![]() 过点
过点![]() 且垂直于矩形
且垂直于矩形![]() 所在平面,点
所在平面,点![]() 是直线
是直线![]() 上的一个动点,且与点
上的一个动点,且与点![]() 位于平面
位于平面![]() 的同侧。
的同侧。
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 的平面角为
的平面角为![]() ,若
,若![]() ,求线段
,求线段![]() 长的取值范围。
长的取值范围。


21.已知A,B是椭圆![]() 的左,右顶点,
的左,右顶点,![]() ,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线
,过椭圆C的右焦点F的直线交椭圆于点M,N,交直线![]() 于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
于点P,且直线PA,PF,PB的斜率成等差数列,R和Q是椭圆上的两动点,R和Q的横坐标之和为2,RQ的中垂线交X轴于T点
(1)求椭圆C的方程;
 (2)求三角形MNT的面积的最大值
(2)求三角形MNT的面积的最大值
22. 已知函数![]()
![]() ,
,
(Ⅰ)若![]() 在
在![]() 上存在最大值与最小值,且其最大值与最小值的和为
上存在最大值与最小值,且其最大值与最小值的和为![]() ,试求
,试求![]() 和
和![]() 的值。
的值。
(Ⅱ)若![]() 为奇函数:
为奇函数:
(1)是否存在实数![]() ,使得
,使得![]() 在
在![]() 为增函数,
为增函数,![]() 为减函数,若存在,求出
为减函数,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)如果当![]() 时,都有
时,都有![]() 恒成立,试求
恒成立,试求![]() 的取值范围.
的取值范围.
 ,
, 不等式恒成立,求
不等式恒成立,求 的取值范围;
的取值范围; 的一切
的一切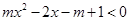 ,
,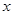 不等式恒成立,求
不等式恒成立,求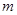 的取值范围;
的取值范围;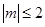 的一切
的一切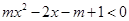 ,
,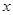 不等式恒成立,求
不等式恒成立,求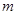 的取值范围;
的取值范围;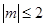 的一切
的一切