摘要:因为有λ>3.0m的条件.所以取n=0.1
网址:http://m.1010jiajiao.com/timu_id_284791[举报]
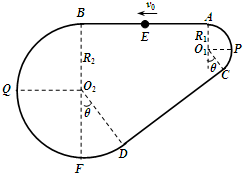 如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:光滑水平直轨AB,半径分别为R1=1.0m和R2=3.0m的光滑弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切.有质量为m=2kg的小球穿在滑轨上,小球与CD杆间的动摩擦因数为μ=
如图是放置在竖直平面内游戏滑轨的模拟装置,滑轨由四部分粗细均匀的金属杆组成:光滑水平直轨AB,半径分别为R1=1.0m和R2=3.0m的光滑弧形轨道,倾斜直轨CD长为L=6m,AB、CD与两圆形轨道相切.有质量为m=2kg的小球穿在滑轨上,小球与CD杆间的动摩擦因数为μ=| 1 | 6 |
求:(1)小球第一次通过O2弧形轨道的最低点F处时对轨道的压力;
(2)小球从E点开始运动后整个运动过程中,经过C 点的次数.
如图所示,一位质量m=60kg参加“挑战极限”的业余选手,要越过一宽度为s=3.0m的水沟,跃上高为h=2.2m的平台,采用的方法是:人手握一根长L=4.0m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变、同时脚蹬地,人被弹起,到达最高点时杆处于竖直,人的重心在杆的顶端,此刻人放开杆水平飞出,最终趴落到平台上,运动过程中空气阻力可忽略不计.(取g=10m/s2)
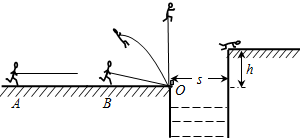
(1)设人到达B点时速度vB=8m/s,人匀加速运动的加速度a=2m/s2,求助跑距离sAB.
(2)人要到达平台,在最高点飞出时刻速度v至少多大?
(3)设人跑动过程中重心离地高度H=0.8m,在(1)、(2)问的条件下,在B点蹬地弹起瞬间,人至少再做多少功?
(4)在前三问条件下,人在刚达到最高点,放手前的瞬间,手和杆之间的摩擦力是多少?
查看习题详情和答案>>

(1)设人到达B点时速度vB=8m/s,人匀加速运动的加速度a=2m/s2,求助跑距离sAB.
(2)人要到达平台,在最高点飞出时刻速度v至少多大?
(3)设人跑动过程中重心离地高度H=0.8m,在(1)、(2)问的条件下,在B点蹬地弹起瞬间,人至少再做多少功?
(4)在前三问条件下,人在刚达到最高点,放手前的瞬间,手和杆之间的摩擦力是多少?
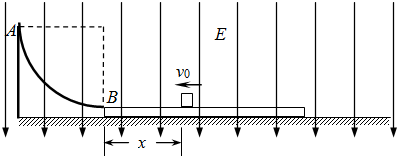 如图所示,在粗糙的水平面上放有质量为M=0.3kg的绝缘长木板,有一质量为m=0.2kg,带电量为q=+4×10-5C的小滑块(可视为质点)正沿木板的上表面向左运动.木板左端有一个固定在水平面上的四分之一光滑圆形绝缘轨道AB与之相接,轨道的最低点B点与木板的上表面相切.整个空间加有一个方向竖直向下、场强大小为E=5×104N/C的匀强电场.已知滑块与木板间的动摩擦因数为μ1=0.25,木板与水平面间的动摩擦因素为μ2=0.1,滑块在木板上向左运动至距离B点x=0.3m处时速度大小为v0=2
如图所示,在粗糙的水平面上放有质量为M=0.3kg的绝缘长木板,有一质量为m=0.2kg,带电量为q=+4×10-5C的小滑块(可视为质点)正沿木板的上表面向左运动.木板左端有一个固定在水平面上的四分之一光滑圆形绝缘轨道AB与之相接,轨道的最低点B点与木板的上表面相切.整个空间加有一个方向竖直向下、场强大小为E=5×104N/C的匀强电场.已知滑块与木板间的动摩擦因数为μ1=0.25,木板与水平面间的动摩擦因素为μ2=0.1,滑块在木板上向左运动至距离B点x=0.3m处时速度大小为v0=2| 3 |
求:
(1)滑块通过木板滑上固定的光滑圆形轨道AB,沿轨道AB上升的最大高度H;
(2)滑块沿轨道AB返回运动至B点的速度vB的大小;
(3)滑块沿轨道AB返回运动滑上木板,要使滑块不从木板上掉下来,木板的长度L至少应为多少?
(4)在满足(3)的条件下,求滑块停止运动时与B点的距离△x是多少?
 (2011?浙江模拟)在竖直面内有一条光滑弯曲轨道,轨道上各个最低点在同一水平线上,弯曲部分都用一小段圆弧相连.一个小环套在轨道上,从3.0m的高处无初速度释放.轨道上各个高点的高度如图所示.关于小环在轨道上的运动,以下说法正确的是(g=10m/s2)( )
(2011?浙江模拟)在竖直面内有一条光滑弯曲轨道,轨道上各个最低点在同一水平线上,弯曲部分都用一小段圆弧相连.一个小环套在轨道上,从3.0m的高处无初速度释放.轨道上各个高点的高度如图所示.关于小环在轨道上的运动,以下说法正确的是(g=10m/s2)( ) 在竖直平面内有一条光滑弯曲轨道,一个小环套在轨道上,从3.0m的高处无初速度释放.轨道上各个高点的高度如图所示.则第
在竖直平面内有一条光滑弯曲轨道,一个小环套在轨道上,从3.0m的高处无初速度释放.轨道上各个高点的高度如图所示.则第