题目内容
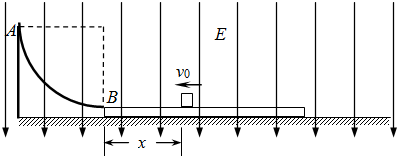 如图所示,在粗糙的水平面上放有质量为M=0.3kg的绝缘长木板,有一质量为m=0.2kg,带电量为q=+4×10-5C的小滑块(可视为质点)正沿木板的上表面向左运动.木板左端有一个固定在水平面上的四分之一光滑圆形绝缘轨道AB与之相接,轨道的最低点B点与木板的上表面相切.整个空间加有一个方向竖直向下、场强大小为E=5×104N/C的匀强电场.已知滑块与木板间的动摩擦因数为μ1=0.25,木板与水平面间的动摩擦因素为μ2=0.1,滑块在木板上向左运动至距离B点x=0.3m处时速度大小为v0=2
如图所示,在粗糙的水平面上放有质量为M=0.3kg的绝缘长木板,有一质量为m=0.2kg,带电量为q=+4×10-5C的小滑块(可视为质点)正沿木板的上表面向左运动.木板左端有一个固定在水平面上的四分之一光滑圆形绝缘轨道AB与之相接,轨道的最低点B点与木板的上表面相切.整个空间加有一个方向竖直向下、场强大小为E=5×104N/C的匀强电场.已知滑块与木板间的动摩擦因数为μ1=0.25,木板与水平面间的动摩擦因素为μ2=0.1,滑块在木板上向左运动至距离B点x=0.3m处时速度大小为v0=2| 3 |
求:
(1)滑块通过木板滑上固定的光滑圆形轨道AB,沿轨道AB上升的最大高度H;
(2)滑块沿轨道AB返回运动至B点的速度vB的大小;
(3)滑块沿轨道AB返回运动滑上木板,要使滑块不从木板上掉下来,木板的长度L至少应为多少?
(4)在满足(3)的条件下,求滑块停止运动时与B点的距离△x是多少?
分析:(1)对于滑块上升到最高点过程,重力、电场力、摩擦力做功,根据动能定理求出滑块上升的最大高度H;
(2)滑块从开始运动到返回至B点处过程,摩擦力和电场力做功,再由动能定理求解速度vB的大小;
(3)滑块沿轨道AB返回运动滑上木板,滑块做匀减速运动,木块做匀加速运动,当两者速度相等时,两者所走的位移之差即为木板的长度的最小值.由牛顿第二定律和运动学公式结合求解.
(4)由几何关系求出滑块停止运动时与B点的距离△x.
(2)滑块从开始运动到返回至B点处过程,摩擦力和电场力做功,再由动能定理求解速度vB的大小;
(3)滑块沿轨道AB返回运动滑上木板,滑块做匀减速运动,木块做匀加速运动,当两者速度相等时,两者所走的位移之差即为木板的长度的最小值.由牛顿第二定律和运动学公式结合求解.
(4)由几何关系求出滑块停止运动时与B点的距离△x.
解答:解:(1)对于滑块上升到最高点过程根据动能定理得:
-μ1(qE+mg)?x-(qE+mg)?H=0-
m
解得:H=
-μ1x=0.225m
(2)对于滑块从开始运动到返回至B点处过程根据动能定理得:
-μ1(qE+mg)?x=
m
-
m
解得:vB=
=3m/s
(3)滑块又滑上木板后做匀减速运动,滑块的加速度为a1=
=5m/s2.
由于f1=μ1(mg+qE)=2N,f2=μ2(qE+mg+Mg)=0.7N,则μ1(mg+qE)>μ2(qE+mg+Mg),所以木板由静止开始做匀加速运动,加速度大小为
a2=
=1m/s2,
设两者经过时间t速度相等,则 vB-a1t=a2t,解得,t=0.5s
速度相等之后,滑块与木板相对静止做匀减速运动直至停止.那么速度相等时,两者所走的位移之差即为木板的长度的最小值,
则在两者相对滑动的过程中,滑块的位移为s1=vBt-
a1t2,木板的位移为s2=
a2t2
木板的长度的最小值为:L=△s=s1-s2,
代入解得,△s=0.75m.
(4)速度相等之后,根据动能定理得
-μ2(mg+Mg+F)s共=0-
(M+m)v2
又 v=a2t.
解得,s共=
m
(4)滑块停止运动时与B点的距离△x=s1+s共=
+
=
m
答:(1)滑块通过木板滑上固定的光滑圆形轨道AB,沿轨道AB上升的最大高度H为0.225m;
(2)滑块沿轨道AB返回运动至B点的速度vB的大小是3m/s;
(3)滑块沿轨道AB返回运动滑上木板,要使滑块不从木板上掉下来,木板的长度L至少应为0.75m.
(4)在满足(3)的条件下,滑块停止运动时与B点的距离△x是
m.
-μ1(qE+mg)?x-(qE+mg)?H=0-
| 1 |
| 2 |
| v | 2 0 |
解得:H=
m
| ||
| 2(qE+mg) |
(2)对于滑块从开始运动到返回至B点处过程根据动能定理得:
-μ1(qE+mg)?x=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 0 |
解得:vB=
|
(3)滑块又滑上木板后做匀减速运动,滑块的加速度为a1=
| μ1(mg+qE) |
| m |
由于f1=μ1(mg+qE)=2N,f2=μ2(qE+mg+Mg)=0.7N,则μ1(mg+qE)>μ2(qE+mg+Mg),所以木板由静止开始做匀加速运动,加速度大小为
a2=
| f1-f2 |
| M |
设两者经过时间t速度相等,则 vB-a1t=a2t,解得,t=0.5s
速度相等之后,滑块与木板相对静止做匀减速运动直至停止.那么速度相等时,两者所走的位移之差即为木板的长度的最小值,
则在两者相对滑动的过程中,滑块的位移为s1=vBt-
| 1 |
| 2 |
| 1 |
| 2 |
木板的长度的最小值为:L=△s=s1-s2,
代入解得,△s=0.75m.
(4)速度相等之后,根据动能定理得
-μ2(mg+Mg+F)s共=0-
| 1 |
| 2 |
又 v=a2t.
解得,s共=
| 5 |
| 56 |
(4)滑块停止运动时与B点的距离△x=s1+s共=
| 7 |
| 8 |
| 5 |
| 56 |
| 27 |
| 28 |
答:(1)滑块通过木板滑上固定的光滑圆形轨道AB,沿轨道AB上升的最大高度H为0.225m;
(2)滑块沿轨道AB返回运动至B点的速度vB的大小是3m/s;
(3)滑块沿轨道AB返回运动滑上木板,要使滑块不从木板上掉下来,木板的长度L至少应为0.75m.
(4)在满足(3)的条件下,滑块停止运动时与B点的距离△x是
| 27 |
| 28 |
点评:本题的关键要耐心细致地分析物体的运动过程,根据木板所受的滑动摩擦力与最大静摩擦力的关系,判断木板的运动状态,运用动能定理、牛顿第二定律和运动学公式结合进行处理.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 (2006?松江区二模)如图所示,在粗糙水平板上放一个物块,使水平板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动.a b为水平直径,c d为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
(2006?松江区二模)如图所示,在粗糙水平板上放一个物块,使水平板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动.a b为水平直径,c d为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( ) 如图所示,在粗糙水平板上放一个物块,使水平板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动.a b为水平直径,c d为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
如图所示,在粗糙水平板上放一个物块,使水平板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动.a b为水平直径,c d为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( ) 如图所示,在粗糙水平板上放一个物块,使水平板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动.a b为水平直径,c d为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
如图所示,在粗糙水平板上放一个物块,使水平板和物块一起在竖直平面内沿逆时针方向做匀速圆周运动.a b为水平直径,c d为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,则( )
