网址:http://m.1010jiajiao.com/timu_id_283274[举报]
一.选择题(本大题共10小题,每小题3分,共30分.每小题只有一个正确答案)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
C
B
A
D
B
B
B
D
二,填空题(本大题共5小题,每小题3分,共15分.把答案填在题中横线上)
11.(1,3); 12.4; 13.(0,1)或(-4,-1); 14 2; 15 85;
三.解答题(本大题共6小题,共55分.解答应写出文字说明,证明过程或演算步骤)
16.(1) ; (4分)(2)21
; (4分)(2)21 ; (8分)
; (8分)
17.解:
①当 时,由
时,由 得
得
 解得
解得 ;
(4分)
;
(4分)
②当 时,
时, ;
;
解得: 。
。

19.解:画散点图
以y= ax+b为拟合函数好
由{ ,解得{
,解得{
所以y= 2x+48.取x=5,y=80,
估计5月份的产量为8万件。 (8分)
20.
解: (1)  的定义域为R, 设
的定义域为R, 设 ,
,
则 =
= ,
,
 ,
,  ,
,
即 ,所以不论
,所以不论 为何实数
为何实数 总为增函数.
(4分)
总为增函数.
(4分)
(2)  为奇函数,
为奇函数,  ,即
,即 ,
,
解得: 
 (7分)
(7分)
(3) 由(2)知 ,
,  ,
, ,
,

所以 的值域为
的值域为 (11分)
(11分)
21. 解:(1)令 ,则由已知
,则由已知
∴ (3分)
(3分)
(2)令 , 则
, 则
又∵
∴ (6分)
(6分)
(3)不等式 即
即
即
当 时,
时, , 又
, 又 恒成立
恒成立
故

又 在
在 上是单调函数,故有
上是单调函数,故有
∴
∴ ∩
∩ =
= (12分)
(12分)
附加题
已知 ,设
,设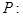
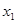 和
和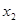 是方程
是方程 的两个根,不等式
的两个根,不等式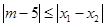 对任意实数
对任意实数 恒成立;
恒成立;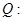 函数
函数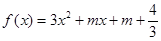 有两个不同的零点.求使“P且Q”为真命题的实数
有两个不同的零点.求使“P且Q”为真命题的实数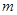 的取值范围.
的取值范围.
【解析】本试题主要考查了命题和函数零点的运用。由题设x1+x2=a,x1x2=-2,
∴|x1-x2|=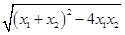 =
=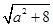 .
.
当a∈[1,2]时,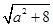 的最小值为3. 当a∈[1,2]时,
的最小值为3. 当a∈[1,2]时,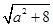 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
可得到要使“P∧Q”为真命题,只需P真Q真即可。
解:由题设x1+x2=a,x1x2=-2,
∴|x1-x2|=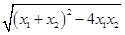 =
=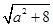 .
.
当a∈[1,2]时,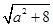 的最小值为3.
的最小值为3.
要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只须|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+ =0的判别式
=0的判别式
Δ=4m2-12(m+ )=4m2-12m-16>0,
)=4m2-12m-16>0,
得m<-1或m>4.
综上,要使“P∧Q”为真命题,只需P真Q真,即
解得实数m的取值范围是(4,8]
查看习题详情和答案>>
(1)求f(0)的值.
(2)求f(x)的解析式.
(3)已知a∈R,设P:当0<x<
| 1 | 2 |
已知:函数 对一切实数
对一切实数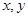 都有
都有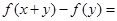
 成立,且
成立,且 .
.
(1)求 的值。
的值。
(2)求 的解析式。
的解析式。
(3)已知 ,设P:当
,设P:当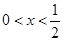 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为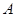 ,满足Q成立的
,满足Q成立的 的集合记为
的集合记为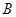 ,求
,求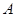 ∩
∩ (
( 为全集)。
为全集)。
查看习题详情和答案>>
 对一切实数
对一切实数 都有
都有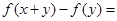
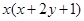 成立,且
成立,且 .
. 的值;
的值; ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足使P成立的
是单调函数。如果满足使P成立的 的集合记为
的集合记为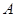 ,满足使Q成立的
,满足使Q成立的 ,求
,求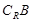 (
( 为全集)。
为全集)。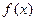 对一切实数
对一切实数 都有
都有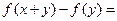
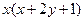 成立,且
成立,且 .
.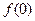 的值。
的值。 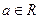 ,设P:当
,设P:当 时,不等式
时,不等式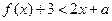 恒成立;Q:当
恒成立;Q:当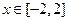 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为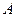 ,满足Q成立的
,满足Q成立的 ,求
,求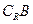 (
(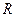 为全集)。
为全集)。