摘要：(Ⅱ)连结AC且交BF于H.可知H是AC中点.连结EH,由E是PC中点,得EH∥PA, PA⊥平面ABCD.
网址：http://m.1010jiajiao.com/timu_id_280487[举报]
已知定点A（0，-1），点B在圆F：x2+（y-1）2=16上运动，F为圆心，线段AB的垂直平分线交BF于P．（I）求动点P的轨迹E的方程；若曲线Q：x2-2ax+y2+a2=1被轨迹E包围着，求实数a的最小值．
（II）已知M（-2，0）、N（2，0），动点G在圆F内，且满足|MG|•|NG|=|OG|2，求
| MG |
| NG |
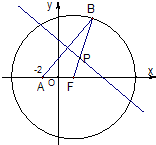已知定点A（-2，0），动点B是圆F：（x-2）2+y2=64（F为圆心）上一点，线段AB的垂直平分线交BF于P．（Ⅰ）求动点P的轨迹方程；
（Ⅱ）是否存在过点E（0，-4）的直线l交P点的轨迹于点R，T，且满足
| OR |
| OT |
| 16 |
| 7 |
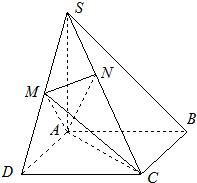如图，在四棱锥S-ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA=AB，点M是SD的中点，AN⊥SC，且交SC于点N．（I）求证：SB∥平面ACM；
（Ⅱ）求二面角D-AC-M的大小；
（Ⅲ）求证：平面SAC⊥平面AMN． 查看习题详情和答案>>
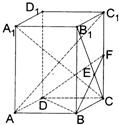已知长方体ABCD-A1B1C1D1中，棱AB=BC=3，BB1=
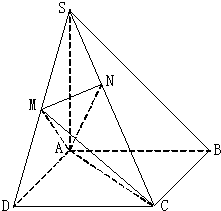如图，在四棱锥S-ABCD中，底面ABCD是正方形，SA⊥底面ABCD，SA=AB，点M是SD的中点，AN⊥SC且交SC于点N．