摘要:(Ⅰ)作.垂足为.连结.由侧面底面.得底面.
网址:http://m.1010jiajiao.com/timu_id_280236[举报]
已知椭圆 :
: 的左焦点
的左焦点 ,若椭圆上存在一点
,若椭圆上存在一点 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段 相切于线段
相切于线段 的中点
的中点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知两点 及椭圆
及椭圆 :
: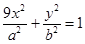 ,过点
,过点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,设线段
两点,设线段 的中点为
的中点为 ,连结
,连结 ,试问当
,试问当 为何值时,直线
为何值时,直线 过椭圆
过椭圆 的顶点?
的顶点?
(Ⅲ) 过坐标原点 的直线交椭圆
的直线交椭圆 :
: 于
于 、
、 两点,其中
两点,其中 在第一象限,过
在第一象限,过 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,连结
,连结 并延长交椭圆
并延长交椭圆 于
于 ,求证:
,求证:
查看习题详情和答案>>
如图13,已知AB为半圆O的直径,AP为过点A的半圆的切线,在 上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E,连结BD,交CE于点F.
上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E,连结BD,交CE于点F.
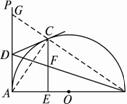
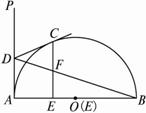
(1) (2)
图13
(1)当点C为![]() 的中点时(如图13(1)),求证:CF =EF;
的中点时(如图13(1)),求证:CF =EF;
(2)当点C不是![]() 的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
 中,AB=BC,以AB为直径的⊙O交AC于点D,过D作
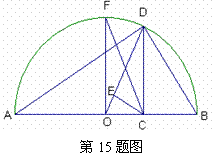
中,AB=BC,以AB为直径的⊙O交AC于点D,过D作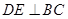 ,垂足为E,连结OE。若
,垂足为E,连结OE。若 ,分别求AB,OE的长。
,分别求AB,OE的长。
 设
设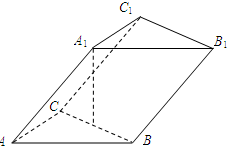 如图:已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,过顶点A1作底面ABC的垂线,若垂足为BC的中点,则异面直线AB与CC1成的角的余弦值为
如图:已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等,过顶点A1作底面ABC的垂线,若垂足为BC的中点,则异面直线AB与CC1成的角的余弦值为