摘要:点到平面的距离为.解法二:
网址:http://m.1010jiajiao.com/timu_id_279987[举报]
如图,在三棱锥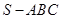 中,平面
中,平面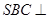 平面
平面 ,
,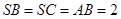 ,
,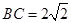 ,
,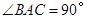 ,
,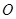 为
为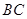 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角 的余弦值.
的余弦值.

【解析】第一问中利用因为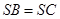 ,
,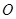 为
为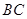 中点,所以
中点,所以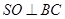
而平面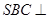 平面
平面 ,所以
,所以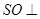 平面
平面 ,再由题设条件知道可以分别以
,再由题设条件知道可以分别以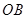 、
、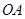 、
、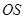 为
为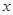 ,
,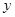 ,
,
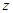 轴建立直角坐标系得
轴建立直角坐标系得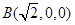 ,
,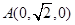 ,
,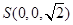 ,
,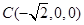 ,
,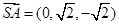 ,
,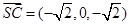 ,
,
故平面 的法向量
的法向量 而
而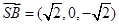 ,故点B到平面
,故点B到平面 的距离
的距离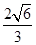
第二问中,由已知得平面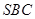 的法向量
的法向量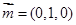 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于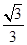
解:(Ⅰ)因为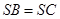 ,
,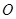 为
为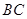 中点,所以
中点,所以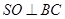
而平面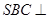 平面
平面 ,所以
,所以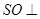 平面
平面 ,
,
再由题设条件知道可以分别以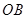 、
、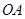 、
、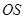 为
为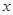 ,
,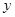 ,
,
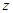 轴建立直角坐标系,得
轴建立直角坐标系,得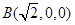 ,
,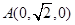 ,
,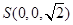 ,
,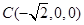 ,
,
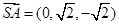 ,
,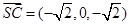 ,故平面
,故平面 的法向量
的法向量
而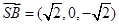 ,故点B到平面
,故点B到平面 的距离
的距离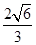
(Ⅱ)由已知得平面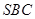 的法向量
的法向量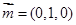 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于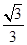
查看习题详情和答案>>
 (2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.
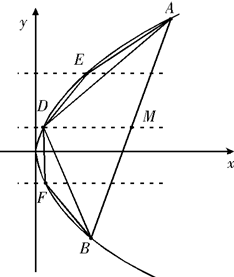
(2007•浦东新区二模)已知抛物线C:y2=2px(p>0)上横坐标为4的点到焦点的距离为5.(1)求抛物线C的方程.
(2)设直线y=kx+b(k≠0)与抛物线C交于两点A(x1,y1),B(x2,y2),且|y1-y2|=a(a>0),M是弦AB的中点,过M作平行于x轴的直线交抛物线C于点D,得到△ABD;再分别过弦AD、BD的中点作平行于x轴的直线依次交抛物线C于点E,F,得到△ADE和△BDF;按此方法继续下去.
解决下列问题:
①求证:a2=
| 16(1-kb) | k2 |
②计算△ABD的面积S△ABD;
③根据△ABD的面积S△ABD的计算结果,写出△ADE,△BDF的面积;请设计一种求抛物线C与线段AB所围成封闭图形面积的方法,并求出此封闭图形的面积.