网址:http://m.1010jiajiao.com/timu_id_277938[举报]
设椭圆  :
: (
( )的一个顶点为
)的一个顶点为 ,
, ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率
 ,过椭圆右焦点
,过椭圆右焦点
 的直线
的直线  与椭圆
与椭圆  交于
交于 ,
, 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)是否存在直线  ,使得
,使得
 ,若存在,求出直线
,若存在,求出直线
 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
【解析】本试题主要考查了椭圆的方程的求解,以及直线与椭圆的位置关系的运用。(1)中椭圆的顶点为 ,即
,即 又因为
又因为 ,得到
,得到 ,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合
,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合 得到结论。
得到结论。
解:(1)椭圆的顶点为 ,即
,即
 ,解得
,解得 ,
,
 椭圆的标准方程为
椭圆的标准方程为 --------4分
--------4分
(2)由题可知,直线 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意. --------5分
②当直线斜率存在时,设存在直线 为
为 ,且
,且 ,
, .
.
由 得
得 , ----------7分
, ----------7分
 ,
, ,
,

=
所以 ,
----------10分
,
----------10分
故直线 的方程为
的方程为 或
或
即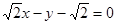 或
或
查看习题详情和答案>>
如图,直线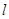 与抛物线
与抛物线 交于
交于 两点,与
两点,与 轴相交于点
轴相交于点 ,且
,且 .
.
(1)求证: 点的坐标为
点的坐标为 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.

【解析】设出点M的坐标 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据 ,即可建立关于
,即可建立关于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)问的基础上,证明: 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
查看习题详情和答案>>
过抛物线

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
【解析】本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
(1)中证明:设 下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得
下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得

(2)中:因为三条直线AN,MN,BN的斜率成等差数列,下证之
设点N(-m,n),则直线AN的斜率KAN= ,直线BN的斜率KBN=
,直线BN的斜率KBN=

KAN+KBN= +
+
本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
查看习题详情和答案>>
某上市股票在30天内每股的交易价格 (元)与时间
(元)与时间 (天)所组成的有序数对
(天)所组成的有序数对 落在下图中的两条线段上,该股票在30天内的日交易量
落在下图中的两条线段上,该股票在30天内的日交易量 (万股)与时间
(万股)与时间 (天)的部分数据如下表所示.
(天)的部分数据如下表所示.

|
第t天 |
4 |
10 |
16 |
22 |
|
Q(万股) |
36 |
30 |
24 |
18 |
⑴根据提供的图象,写出该种股票每股交易价格 (元)与时间
(元)与时间 (天)所满足的函数关系式;
(天)所满足的函数关系式;
⑵根据表中数据确定日交易量 (万股)与时间
(万股)与时间 (天)的一次函数关系式;
(天)的一次函数关系式;
⑶在(2)的结论下,用 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出 关于
关于 的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
的函数关系式,并求这30天中第几天日交易额最大,最大值为多少?
【解析】(1)根据图象可知此函数为分段函数,在(0,20]和(20,30]两个区间利用待定系数法分别求出一次函数关系式联立可得P的解析式;
(2)因为Q与t成一次函数关系,根据表格中的数据,取出两组即可确定出Q的解析式;
(3)根据股票日交易额=交易量×每股较易价格可知y=PQ,可得y的解析式,分别在各段上利用二次函数求最值的方法求出即可.
查看习题详情和答案>>