摘要：(2)方法1:因为对一切实数.都有
网址：http://m.1010jiajiao.com/timu_id_27627[举报]
请阅读下列材料：若两个正实数a1，a2满足a12+a22=1，那么a1+a2≤
．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2≤
．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．
查看习题详情和答案>>
| 2 |
| 2 |
请阅读下列材料：若两个正实数a1，a2满足a12+a22=1，那么a1+a2
．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2
．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．
查看习题详情和答案>>
．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．
查看习题详情和答案>>
请阅读下列材料：若两个正实数a1，a2满足a12+a22=1，那么a1+a2
．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2
．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．
查看习题详情和答案>>
．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．
查看习题详情和答案>>
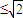．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2
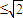．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．
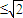．证明：构造函数f（x）=（x-a1）2+（x-a2）2=2x2-2（a1+a2）x+1，因为对一切实数x，恒有f（x）≥0，所以△≤0，从而得4（a1+a2）2-8≤0，所以a1+a2
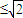．根据上述证明方法，若n个正实数满足a12+a22+…+an2=1时，你能得到的结论为 ．