题目内容
请阅读下列材料:若两个正实数a1,a2满足a12+a22=1,那么a1+a2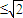 .证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2-8≤0,所以a1+a2
.证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2-8≤0,所以a1+a2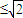 .根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为 .
.根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为 .
【答案】分析:由类比推理知识可构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+1,由对一切实数x,恒有f(x)≥0,所以△≤0,即可得到结论.
解答:解:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+1,
由对一切实数x,恒有f(x)≥0,所以△≤0,得a1+a2+…+an≤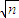
故答案为:a1+a2+…+an≤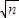
点评:本题考查类比推理、二次函数恒成立知识,考查利用所学知识解决问题的能力.
解答:解:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+1,
由对一切实数x,恒有f(x)≥0,所以△≤0,得a1+a2+…+an≤
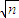
故答案为:a1+a2+…+an≤
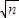
点评:本题考查类比推理、二次函数恒成立知识,考查利用所学知识解决问题的能力.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
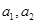 满足
满足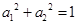 ,那么
,那么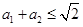 .证明:构造函数
.证明:构造函数 ,因为对一切实数
,因为对一切实数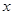 ,恒有
,恒有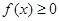 ,所以
,所以 ,从而得
,从而得 ,所以
,所以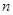 个正实数满足
个正实数满足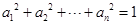 时,你能得到的结论为 .(不必证明)
时,你能得到的结论为 .(不必证明)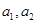 满足
满足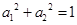 ,那么
,那么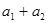 ≤
≤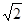 .
.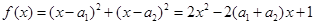 ,因为对一切实数
,因为对一切实数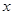 ,恒有
,恒有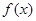 ≥0,所以△≤0,从而得
≥0,所以△≤0,从而得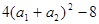 ≤0,所以
≤0,所以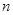 个正实数满足
个正实数满足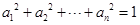 时,你能得到的结论为 ▲ .
时,你能得到的结论为 ▲ . 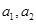 满足
满足 ,那么
,那么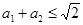 。证明:构造函数
。证明:构造函数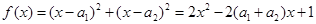 ,因为对一切实数x,恒有
,因为对一切实数x,恒有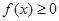 ,所以
,所以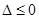 ,从而得
,从而得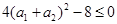 ,所以
,所以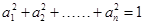 时,你能得到的结论为
。
时,你能得到的结论为
。