题目内容
已知函数g(x)=ax2-2ax+1+b(a>0),在区间[2,3]上有最大值4,最小值1,设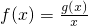 .
.
(Ⅰ)求a、b的值;
(Ⅱ)若不等式f(x)-kx≥0在x∈(0,+∞)时恒成立,求实数k的取值范围;
(Ⅲ)方程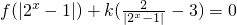 有三个不同的实数解,求实数k的取值范围.
有三个不同的实数解,求实数k的取值范围.
解:(Ⅰ)g(x)=a(x-1)2+1+b-a(a>0),
当a>0时,g(x)在区间[2,3]上为增函数,
故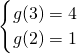 ,即
,即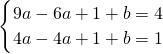 ,解得
,解得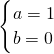 ------
------
(Ⅱ)f(x)-kx≥0化为:x+ -2≥kx,
-2≥kx,
∵x>0,
∴1+ -
- ≥k,
≥k,
∵1+ -
- =
=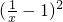 ≥0(当x=1时取等号)
≥0(当x=1时取等号)
∴k≤0.----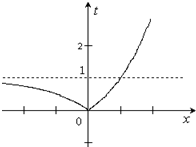
(Ⅲ)方程f(|2x-1|)+k(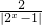 -3)=0可化为:
-3)=0可化为:
|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,|2x-1|≠0,
令|2x-1|=t,则方程化为
t2-(2+3k)t+(1+2k)=0(t≠0),
∵方程|2x-1|+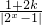 -(2+3k)=0有三个不同的实数解,
-(2+3k)=0有三个不同的实数解,
∴由t=|2x-1|的图象知,
t2-(2+3k)t+(1+2k)=0(t≠0),有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1.
记φ(t)=t2-(2+3k)t+(1+2k),
则 或
或 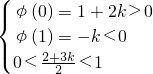
∴k>0------
分析:(Ⅰ)由g(x)=a(x-1)2+1+b-a(a>0)在[2,3]上为增函数,可得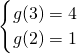 ,从而可求得a、b的值;
,从而可求得a、b的值;
(Ⅱ)f(x)-kx≥0在x∈(0,+∞)时恒成立?k≤1+ -
- =
=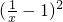 (x>0)恒成立,从而可求得实数k的取值范围;
(x>0)恒成立,从而可求得实数k的取值范围;
(Ⅲ)方程f(|2x-1|)+k(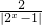 -3)=0?|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,(|2x-1|≠0),令|2x-1|=t,则t2-(2+3k)t+(1+2k)=0(t≠0),构造函数φ(t)=t2-(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围.
-3)=0?|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,(|2x-1|≠0),令|2x-1|=t,则t2-(2+3k)t+(1+2k)=0(t≠0),构造函数φ(t)=t2-(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围.
点评:本题考查二次函数在闭区间上的最值,考查函数恒成立问题问题,考查数形结合与等价转化、函数与方程思想的综合应用,属于难题.
当a>0时,g(x)在区间[2,3]上为增函数,
故
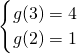 ,即
,即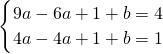 ,解得
,解得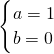 ------
------(Ⅱ)f(x)-kx≥0化为:x+
 -2≥kx,
-2≥kx,∵x>0,
∴1+
 -
- ≥k,
≥k,∵1+
 -
- =
=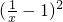 ≥0(当x=1时取等号)
≥0(当x=1时取等号)∴k≤0.----

(Ⅲ)方程f(|2x-1|)+k(
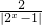 -3)=0可化为:
-3)=0可化为:|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,|2x-1|≠0,
令|2x-1|=t,则方程化为
t2-(2+3k)t+(1+2k)=0(t≠0),
∵方程|2x-1|+
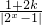 -(2+3k)=0有三个不同的实数解,
-(2+3k)=0有三个不同的实数解,∴由t=|2x-1|的图象知,
t2-(2+3k)t+(1+2k)=0(t≠0),有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1.
记φ(t)=t2-(2+3k)t+(1+2k),
则
 或
或 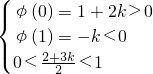
∴k>0------
分析:(Ⅰ)由g(x)=a(x-1)2+1+b-a(a>0)在[2,3]上为增函数,可得
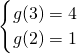 ,从而可求得a、b的值;
,从而可求得a、b的值;(Ⅱ)f(x)-kx≥0在x∈(0,+∞)时恒成立?k≤1+
 -
- =
=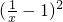 (x>0)恒成立,从而可求得实数k的取值范围;
(x>0)恒成立,从而可求得实数k的取值范围;(Ⅲ)方程f(|2x-1|)+k(
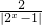 -3)=0?|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,(|2x-1|≠0),令|2x-1|=t,则t2-(2+3k)t+(1+2k)=0(t≠0),构造函数φ(t)=t2-(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围.
-3)=0?|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,(|2x-1|≠0),令|2x-1|=t,则t2-(2+3k)t+(1+2k)=0(t≠0),构造函数φ(t)=t2-(2+3k)t+(1+2k),通过数形结合与等价转化的思想即可求得k的范围.点评:本题考查二次函数在闭区间上的最值,考查函数恒成立问题问题,考查数形结合与等价转化、函数与方程思想的综合应用,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目