摘要:令.得: .
网址:http://m.1010jiajiao.com/timu_id_262485[举报]
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
如图,设A是由n×n个实数组成的n行n列的数表,其中aij(i,j=1,2,3…,n)表示位于第i行第j列的实数,且aij∈{1,-1}.记S(n,n)为所有这样的数表构成的集合.
对于A∈S(n,n),记ri(A)为A的第i行各数之积,Cj(A)为A的第j列各数之积.令l(A)=
ri(A)+
Cj(A).
(Ⅰ)对如下数表A∈S(4,4),求l(A)的值;
(Ⅱ)证明:存在A∈S(n,n),使得l(A)=2n-4k,其中k=0,1,2,…,n;
(Ⅲ)给定n为奇数,对于所有的A∈S(n,n),证明:l(A)≠0.
查看习题详情和答案>>
| a11 | a12 | … | a1n |
| a21 | a22 | … | a2n |
| • • • |
• • • |
… | • • • |
| an1 | an2 | … | ann |
| n |
 |
| i=1 |
| n |
 |
| j=1 |
(Ⅰ)对如下数表A∈S(4,4),求l(A)的值;
| 1 | 1 | -1 | -1 |
| 1 | -1 | 1 | 1 |
| 1 | -1 | -1 | 1 |
| -1 | -1 | 1 | 1 |
(Ⅲ)给定n为奇数,对于所有的A∈S(n,n),证明:l(A)≠0.
如图,设A是由n×n个实数组成的n行n列的数表,其中aij(i,j=1,2,3…,n)表示位于第i行第j列的实数,且aij∈{1,-1}.记S(n,n)为所有这样的数表构成的集合.
对于A∈S(n,n),记ri(A)为A的第i行各数之积,Cj(A)为A的第j列各数之积.令l(A)= ri(A)+
ri(A)+ Cj(A).
Cj(A).
(Ⅰ)对如下数表A∈S(4,4),求l(A)的值;
(Ⅱ)证明:存在A∈S(n,n),使得l(A)=2n-4k,其中k=0,1,2,…,n;
(Ⅲ)给定n为奇数,对于所有的A∈S(n,n),证明:l(A)≠0.
查看习题详情和答案>>
| a11 | a12 | … | a1n |
| a21 | a22 | … | a2n |
| • • • | • • • | … | • • • |
| an1 | an2 | … | ann |
 ri(A)+
ri(A)+ Cj(A).
Cj(A).(Ⅰ)对如下数表A∈S(4,4),求l(A)的值;
| 1 | 1 | -1 | -1 |
| 1 | -1 | 1 | 1 |
| 1 | -1 | -1 | 1 |
| -1 | -1 | 1 | 1 |
(Ⅲ)给定n为奇数,对于所有的A∈S(n,n),证明:l(A)≠0.
查看习题详情和答案>>
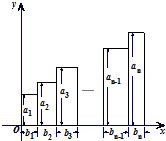 13、已知a1,a2,…,an;b1,b2,…,bn(n是正整数),令L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、某人用右图分析得到恒等式:a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn,则ck=
13、已知a1,a2,…,an;b1,b2,…,bn(n是正整数),令L1=b1+b2+…+bn,L2=b2+b3+…+bn,…,Ln=bn、某人用右图分析得到恒等式:a1b1+a2b2+…+anbn=a1L1+c2L2+c3L3+…+ckLk+…+…+cnLn,则ck=