摘要：所以 当时.取最大值 1 .
网址：http://m.1010jiajiao.com/timu_id_262460[举报]
设f（x）=x3-ax2-bx-c，x∈[-1，1]，记y=|f（x）|的最大值为M．
（Ⅰ）当a=c=0，b=
时，求M的值；
（Ⅱ）当a，b，c取遍所有实数时，求M的最小值．
（以下结论可供参考：对于a，b，c，d∈R，有|a+b+c+d|≤|a|+|b|+|c|+|d|，当且仅当a，b，c，d同号时取等号） 查看习题详情和答案>>
（Ⅰ）当a=c=0，b=
| 3 | 4 |
（Ⅱ）当a，b，c取遍所有实数时，求M的最小值．
（以下结论可供参考：对于a，b，c，d∈R，有|a+b+c+d|≤|a|+|b|+|c|+|d|，当且仅当a，b，c，d同号时取等号） 查看习题详情和答案>>
设f（x）=x3-ax2-bx-c，x∈[-1，1]，记y=|f（x）|的最大值为M．
（Ⅰ）当a=c=0，b=
时，求M的值；
（Ⅱ）当a，b，c取遍所有实数时，求M的最小值．
（以下结论可供参考：对于a，b，c，d∈R，有|a+b+c+d|≤|a|+|b|+|c|+|d|，当且仅当a，b，c，d同号时取等号）
查看习题详情和答案>>
（Ⅰ）当a=c=0，b=
| 3 |
| 4 |
（Ⅱ）当a，b，c取遍所有实数时，求M的最小值．
（以下结论可供参考：对于a，b，c，d∈R，有|a+b+c+d|≤|a|+|b|+|c|+|d|，当且仅当a，b，c，d同号时取等号）
已知一非零向量数列{
}满足
＝(1，1)＝(xn，yn)＝
(xn－１－yn－1，xn－1＋yn－1)(n≥2且n∈N*)．给出以下结论：
①数列{||}是等差数列，②
；③设cn＝2log2||，则数列{cn}的前n项和为Tn，当且仅当n＝2时，Tn取得最大值；④记向量与
的夹角为
n(n≥2)，均有n＝
．其中所有正确结论的序号是________
已知一非零向量数列{an}满足a1=（1，1）an=(xn，yn)=
(xn-1-yn-1，xn-1+yn-1)（n≥2且n∈N*）．给出以下结论：
①数列{|an|}是等差数列，②|a1|•|a5|=
；③设cn=2log2|an|，则数列{cn}的前n项和为Tn，当且仅当n=2时，Tn取得最大值；④记向量an与an-1的夹角为θn（n≥2），均有θn=
．其中所有正确结论的序号是 ．
查看习题详情和答案>>
| 1 |
| 2 |
①数列{|an|}是等差数列，②|a1|•|a5|=
| 1 |
| 2 |
| π |
| 4 |
已知函数
，
.
（Ⅰ）若函数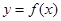
依次在
处取到极值.求
的取值范围；
（Ⅱ）若存在实数
，使对任意的
，不等式
恒成立.求正整数
的最大值.
【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中，利用存在实数，使对任意的，不等式
恒成立转化为
，恒成立，分离参数法求解得到范围。
解：（1）
①
（2）不等式 ，即
，即
.
转化为存在实数
，使对任意的
，不等式恒成立.
即不等式
在上恒成立.
即不等式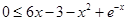
在上恒成立.
设
，则.
设
，则
，因为，有
.
故
在区间上是减函数。又
故存在
，使得
.
当
时，有
，当
时，有
.
从而
在区间
上递增，在区间
上递减.
又
[来源:]
所以当
时，恒有
；当
时，恒有
；
故使命题成立的正整数m的最大值为5
查看习题详情和答案>>