网址:http://m.1010jiajiao.com/timu_id_259216[举报]
若函数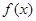 在定义域内存在区间
在定义域内存在区间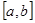 ,满足
,满足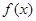 在
在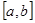 上的值域为
上的值域为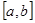 ,则称这样的函数
,则称这样的函数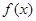 为“优美函数”.
为“优美函数”.
(Ⅰ)判断函数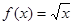 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出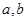 ;若不是,说明理由;
;若不是,说明理由;
(Ⅱ)若函数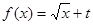 为“优美函数”,求实数
为“优美函数”,求实数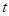 的取值范围.
的取值范围.
【解析】第一问中,利用定义,判定由题意得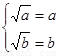 ,由
,由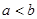 ,所以
,所以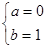
第二问中, 由题意得方程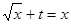 有两实根
有两实根
设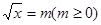 所以关于m的方程
所以关于m的方程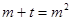 在
在 有两实根,
有两实根,
即函数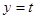 与函数
与函数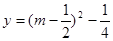 的图像在
的图像在 上有两个不同交点,从而得到t的范围。
上有两个不同交点,从而得到t的范围。
解(I)由题意得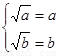 ,由
,由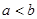 ,所以
,所以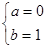 (6分)
(6分)
(II)由题意得方程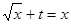 有两实根
有两实根
设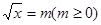 所以关于m的方程
所以关于m的方程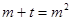 在
在 有两实根,
有两实根,
即函数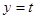 与函数
与函数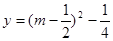 的图像在
的图像在 上有两个不同交点。
上有两个不同交点。
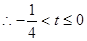
查看习题详情和答案>>
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线 的焦点为F1.
的焦点为F1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.
【解析】本试题主要考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。第一问中,设出椭圆的方程,然后结合抛物线的焦点坐标得到 ,又因为
,又因为 ,这样可知得到
,这样可知得到 。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
。第二问中设直线l的方程为y=-x+m与椭圆联立方程组可以得到
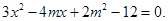 ,再利用
,再利用 可以结合韦达定理求解得到m的值和圆p的方程。
可以结合韦达定理求解得到m的值和圆p的方程。
解:(Ⅰ)设椭圆E的方程为
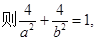 ①………………………………1分
①………………………………1分

 ②………………2分
②………………2分
 ③ 由①、②、③得a2=12,b2=6…………3分
③ 由①、②、③得a2=12,b2=6…………3分
所以椭圆E的方程为 …………………………4分
…………………………4分
(Ⅱ)依题意,直线OC斜率为1,由此设直线l的方程为y=-x+m,……………5分
代入椭圆E方程,得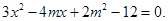 …………………………6分
…………………………6分
 ………………………7分
………………………7分
 、
、 ………………8分
………………8分

 ………………………9分
………………………9分

 ……………………………10分
……………………………10分
当m=3时,直线l方程为y=-x+3,此时,x1 +x2=4,圆心为(2,1),半径为2,
圆P的方程为(x-2)2+(y-1)2=4;………………………………11分
同理,当m=-3时,直线l方程为y=-x-3,
圆P的方程为(x+2)2+(y+1)2=4
查看习题详情和答案>>
如图,已知点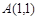 和单位圆上半部分上的动点B.
和单位圆上半部分上的动点B.
(1)若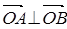 ,求向量
,求向量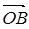 ;
;
(2)求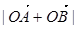 的最大值.
的最大值.
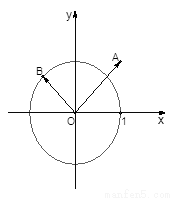
【解析】对于这样的向量的坐标和模最值的求解,利用建立直角坐标系的方法可知。
第一问中,依题意,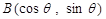 ,
,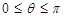
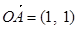 ,
,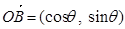
因为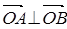 ,所以
,所以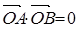 ,即
,即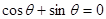 ,
,
解得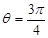 ,所以
,所以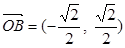
第二问中,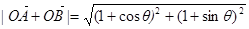 结合三角函数的性质得到最值。
结合三角函数的性质得到最值。
(1)依题意,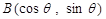 ,
,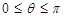 (不含1个或2个端点也对)
(不含1个或2个端点也对)
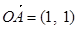 ,
,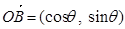 (写出1个即可)
(写出1个即可)
因为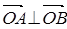 ,所以
,所以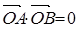 ,即
,即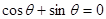 ,
,
解得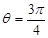 ,所以
,所以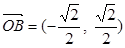 .-
.-
(2)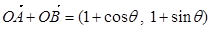 ,
,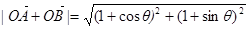
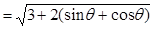
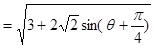 当
当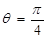 时,
时,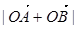 取得最大值,
取得最大值,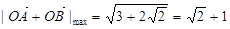
查看习题详情和答案>>
设函数f(x)= 在[1,+∞
在[1,+∞ 上为增函数.
上为增函数.
(1)求正实数a的取值范围;
(2)比较 的大小,说明理由;
的大小,说明理由;
(3)求证: (n∈N*, n≥2)
(n∈N*, n≥2)
【解析】第一问中,利用
解:(1)由已知: ,依题意得:
,依题意得: ≥0对x∈[1,+∞
≥0对x∈[1,+∞ 恒成立
恒成立
∴ax-1≥0对x∈[1,+∞ 恒成立 ∴a-1≥0即:a≥1
恒成立 ∴a-1≥0即:a≥1
(2)∵a=1 ∴由(1)知:f(x)= 在[1,+∞)上为增函数,
在[1,+∞)上为增函数,
∴n≥2时:f( )=
)=
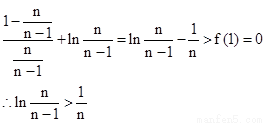
(3) ∵ ∴
∴
查看习题详情和答案>>
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
【解析】第一问当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
第二问当 时,
时, ,令
,令 得
得 ,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
,结合导数和函数之间的关系得到单调性的判定,得到极值和最值
第三问假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
(Ⅰ)当 时,
时, ,则
,则 。
。
依题意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①当 时,
时, ,令
,令 得
得
当 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
极小值 |
单调递增 |
极大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值为2.
上的最大值为2.
②当 时,
时,  .当
.当 时,
时,  ,
, 最大值为0;
最大值为0;
当 时,
时,  在
在 上单调递增。∴
上单调递增。∴ 在
在 最大值为
最大值为 。
。
综上,当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为2;
上的最大值为2;
当 时,即
时,即 时,
时, 在区间
在区间 上的最大值为
上的最大值为 。
。
(Ⅲ)假设曲线 上存在两点P、Q满足题设要求,则点P、Q只能在
上存在两点P、Q满足题设要求,则点P、Q只能在 轴两侧。
轴两侧。
不妨设 ,则
,则 ,显然
,显然
∵ 是以O为直角顶点的直角三角形,∴
是以O为直角顶点的直角三角形,∴
即 (*)若方程(*)有解,存在满足题设要求的两点P、Q;
(*)若方程(*)有解,存在满足题设要求的两点P、Q;
若方程(*)无解,不存在满足题设要求的两点P、Q.
若 ,则
,则 代入(*)式得:
代入(*)式得:
即 ,而此方程无解,因此
,而此方程无解,因此 。此时
。此时 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,则
,则
∴ 在
在 上单调递增, ∵
上单调递增, ∵  ∴
∴ ,∴
,∴ 的取值范围是
的取值范围是 。
。
∴对于 ,方程(**)总有解,即方程(*)总有解。
,方程(**)总有解,即方程(*)总有解。
因此,对任意给定的正实数 ,曲线
,曲线 上存在两点P、Q,使得
上存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上
轴上
查看习题详情和答案>>





 单调递减
单调递减