摘要:∴.即-------10分
网址:http://m.1010jiajiao.com/timu_id_256724[举报]
(10分)在一次国际大型体育运动会上,某运动员报名参加了其中5个项目的比赛.已知该运动员在这5个项目中,每个项目能打破世界纪录的概率都是0.8,那么在本次运动会上:
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为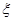 ,求
,求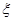 的数学期望
的数学期望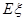 (即均值).
(即均值).
查看习题详情和答案>>
(10分)在一次国际大型体育运动会上,某运动员报名参加了其中5个项目的比赛.已知该运动员在这5个项目中,每个项目能打破世界纪录的概率都是0.8,那么在本次运动会上:
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为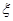 ,求
,求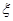 的数学期望
的数学期望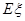 (即均值).
(即均值).
(1)求该运动员至少能打破3项世界纪录的概率;
(2)若该运动员能打破世界纪录的项目数为
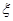 ,求
,求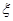 的数学期望
的数学期望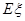 (即均值).
(即均值).(满分13分) 深圳某商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
|
资金 |
每台空调或冰箱所需资金(百元) |
月资金供应数量 (百元) |
|
|
空调 |
冰箱 |
||
|
成本 |
30 |
20 |
300 |
|
工人工资 |
5 |
10 |
110 |
|
每台利润 |
6 |
8 |
|
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?
查看习题详情和答案>>
 节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.
节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.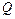 与周次t之间的关系为
与周次t之间的关系为 ,
,